题目内容
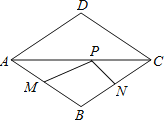
【题目】如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.
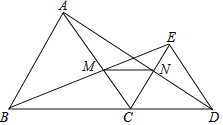
(1)AD与BE有什么数量关系,并证明你的结论.
(2)求证:△MNC是等边三角形.
【答案】(1)BE=AD,见解析;(2)见解析.
【解析】
(1)依据等边三角形的性质可得到BE=AD,CE=CD,∠ACB=∠ECD=60°,然后可证明∠ACD=∠BCE=120°,依据SAS可证明△BCE≌△ACD,最后依据全等三角形的性质可得到BE=AD;
(2)证明△BCM≌△ACN,从而得到MC=CN,然后证明∠MCN=60°即可.
(1)BE=AD.理由如下:
∵∠BCA=∠DCE=60°,∴∠BCE=∠ACD.
在△BCE和△ACD中,∵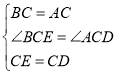 ,∴△BCE≌△ACD(SAS),∴BE=AD;
,∴△BCE≌△ACD(SAS),∴BE=AD;
(2)∵△BCE≌△ACD,∴∠CBM=∠CAN.
∵∠ACB=∠DCE=60°,∴∠ACN=60°,∴∠BCM=∠ACN.
在△BCM和△ACN中,∵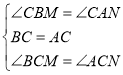 ,∴△BCM≌△ACN(ASA),∴CM=CN.
,∴△BCM≌△ACN(ASA),∴CM=CN.
∵∠ACN=60°,∴△CMN是等边三角形.

练习册系列答案
相关题目