题目内容
【题目】已知![]() ,
, ![]() .
.
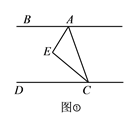
(1)如图①,当![]() 平分
平分![]() 时,求证:
时,求证: ![]() 平分
平分![]() ;
;
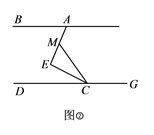
(2)如图②,移动直角顶点![]() ,使
,使![]() ,求证:
,求证: ![]() .
.
【答案】证明见解析.
【解析】试题分析:(1)由CE平分∠ACD可得出∠ACE=∠ECD,因为∠AEC=90°,所以∠EAC+∠ACE=90°,所以∠EAC+∠ECD=90°,又因为AB∥CD,所以∠BAC+∠ACD=180°,所以∠BAE+∠ECD=90°,所以∠EAC=∠BAE即AE平分∠BAC;(2)延长AE交DG于点F,
由∠MCE=∠ECF,∠MEC=∠FEC=90°结合三角形内角和可得出∠CME=∠CFE,进而得出∠MCG=2∠EFC,又因为AB∥CD,所以∠BAE=∠EFC,所以∠MCG=2∠BAE.
试题解析:
(1)∵CE平分∠ACD,
∴∠ACE=∠ECD,
∵∠AEC=90°,
∴∠EAC+∠ACE=90°,
∴∠EAC+∠ECD=90°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠BAE+∠ECD=90°,
∴∠EAC=∠BAE,
∴AE平分∠BAC;
(2)延长AE交DG于点F,
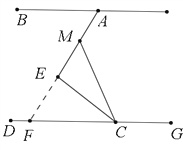
∵∠MCE=∠ECF,∠MEC=∠FEC=90°,
∴∠CME=∠CFE,
∴∠MCG=2∠EFC,
∵AB∥CD,
∴∠BAE=∠EFC,
∵∠MCG=2∠BAE.

练习册系列答案
相关题目