��Ŀ����
����Ŀ�����壺��һ��Ա���һ���Խ��߾���ȵ��ı���Ϊ�Ե��ı��Σ������Խ����ֳƶԵ��ߣ�
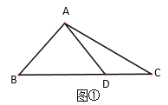
��1����ͼ1�����ı���ABCD�У���C����BDC��EΪAB���е㣬DE��AB����֤���ı���ABCD�ǶԵ��ı��Σ�
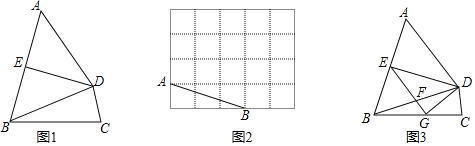
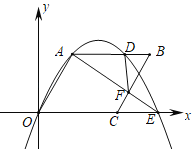
��2����ͼ2����5��4�ķ���ֽ�У�A��B�ڸ���ϣ��뻭��һ�����������ĶԵ��ı���ABCD��ʹBD�ǶԵ��ߣ�C��D�ڸ���ϣ�
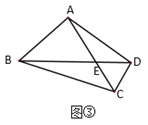
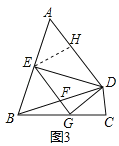
��3����ͼ3����ͼ��1���������£�����E��AD��ƽ���߽�BD��BC�ڵ�F��G������DG����DG��EG��DG��2��AB��5����Ե���BD�ij���
���𰸡���1������������2������������3��BD��![]() ��
��
��������
��1����˵����C=��BDC��֤��BC=BD��Ȼ���ɵ��������ε����ʵõ�BD=AD������֤����
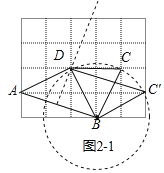
��2����A B�Ĵ�ֱƽ�����뷽��ֽ�ϵĸ��Ľ��㼴Ϊ��D�����Ե�BΪԲ�ġ���BD��Ϊ�뾶��Բ��Բ�뷽��ֽ�ϵĸ��Ľ��㼴Ϊ��C������AD��BC��CD����AD=BC=BD���������ͼ��
��3������E��EH��AD��H����֤���ı���DGEH�Ǿ��Σ��ó�EH=DG=2��Ȼ�������AE�ij�����S��ADE=S��BDE����DE=x��A D=BD=y��Ȼ�������ù��ɶ����������ε������ʽ�г���������⼴�ɣ�
��1��֤�����ߡ�C����BDC��
��BC��BD��
��EΪAB���е㣬DE��AB��
��BD��AD��
��BC��AD��BD��
���ı���ABCD�ǶԵ��ı��Σ�
��2���⣺�����ֻ�����
��AB�Ĵ�ֱƽ�����뷽��ֽ�ϵĸ��Ľ��㼴Ϊ��D�����Ե�BΪԲ�ġ���BD��Ϊ�뾶��Բ��Բ�뷽��ֽ�ϵĸ��Ľ��㼴Ϊ��C������AD��BC��CD����AD��BC��BD����ͼ2��1��ʾ��
��3���⣺����E��EH��AD��H����ͼ3��ʾ��
���EHD��90�㣬
��EG��AD��DG��EG��
���EGD����HDG��90�㣬
���ı���DGEH�Ǿ��Σ�
��EH��DG��2��
��EΪAB���е㣬AB��5��
��AE��BE��![]() AB��
AB��![]() ��S��ADE��S��BDE��
��S��ADE��S��BDE��
��DE��x��AD��BD��y��
��S��ADE��![]() EHAD��
EHAD��![]() ��2��y��y��S��BDE��
��2��y��y��S��BDE��![]() BEDE��
BEDE��![]() ��
��![]() ��x��
��x��![]() x��
x��
����Rt��BDE�У���BED��90�㣬
��BD2��BE2+DE2����y2����![]() ��2+x2��
��2+x2��
��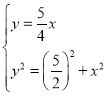 ��
��
��ã�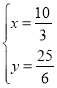
��BD��![]() ��
��

 ȫ��������ϵ�д�
ȫ��������ϵ�д�