Question

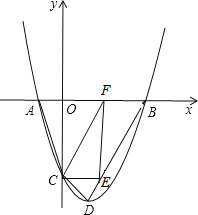
【题目】如图，在平面直角坐标系中，菱形OABC的边长为2，∠AOC＝60°，点D为AB边上的一点，经过O，A，D三点的抛物线与x轴的正半轴交于点E，连结AE交BC于点F，当DF⊥AB时，CE的长为__．

Answer 1

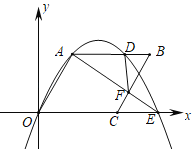
【答案】．

【解析】

设BF=x，则CF=2-x，先确定A、B的坐标，然后再由菱形的性质确定D的坐标，由于抛物线经过O、A、D、E，根据抛物线的对称性可知点A与点D的中点横坐标与点O与点E的中点横坐标相同，可求E，再由平行线等分线段定理列方程求得x，进而求得CE．

解：∵菱形OABC的边长为2，∠AOC＝60°，

∴OA＝2，

∴A（1，），

∵菱形OABC，

∴AB＝OC＝2，AB∥OC，

∴B（3，），

设BF＝x，则CF＝2﹣x，

在菱形OABC中，∠B＝∠AOC＝60°，

∵DF⊥AB，

∴D（3﹣x，），

∴点A与点D的中点为（2﹣x，），

∵抛物线经过O，A，D、E，

∴点O与点E的中点为（2﹣x，0），

∴E（4﹣x，0），

∴CE＝4﹣x﹣2＝2﹣x，

∵AB∥CE，

∴＝，

∴＝，

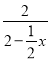∴x＝4+2（舍）或x＝4﹣2，

∴CE＝．

故答案为．