题目内容
【题目】如图,点![]() 为等边三角形
为等边三角形![]() 内一点,且
内一点,且![]() ,则
,则![]() 的最小值为______.
的最小值为______.

【答案】![]()
【解析】
以CD为边在CD的右侧作等边三角形CDE,连接AE,结合等边三角形ABC可证△ACE≌△BCD,进而可证得∠AED=∠AEC-∠CED=60°,过点A作AF⊥BE于点F,利用三角函数还可求得![]() ,再根据AD与AF的大小关系可得
,再根据AD与AF的大小关系可得![]() 即
即![]() ,进而求得答案.
,进而求得答案.
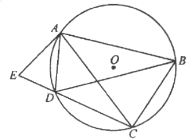
解:如图,以CD为边在CD的右侧作等边三角形CDE,连接AE,

∵△CDE和△ABC为等边三角形,
∴CD=CE,AC=BC,∠DCE=∠ACB=∠CDE=∠CED=60°,
∵∠BDC=120°,
∴∠BDC+∠CDE=180°,
∴点B、D、E在同一直线上,
∵∠DCE=∠ACB,
∴∠DCE-∠ACD=∠ACB-∠ACD,
即∠ACE=∠BCD,
在△ACE与△BCD中,

∴△ACE≌△BCD(SAS),
∴AE=BD,∠AEC=∠BDC=120°,
∴∠AED=∠AEC-∠CED=60°,
过点A作AF⊥BE于点F,
在Rt△AFE中,sin∠AEF=![]() ,
,
则sin60°=![]() ,
,
当点D不与点F重合时,AD>AF,
则![]() ,
,
当点D与点F重合时,AD=AF,
则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的最小值为
的最小值为![]() ,
,
故答案为:![]() .
.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目