题目内容
 已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.
已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.
操作:在图12中作OE⊥OD交AC于E,连接DE.
探究OD、BD、CD三条线段之间有何等量关系?请探究说明.
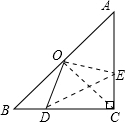 解:如图,关系为2OD2=BD2+CD2.
解:如图,关系为2OD2=BD2+CD2.作OE⊥OD交AC于E,连接OC,DE,得到△OBD≌△OEC
从而Rt△DCE与Rt△ODE中,CE2+DC2=DE2,OD2+OE2=DE2
由BD=CE,OD=OE,所以2OD2=BD2+CD2,(也可过O作BC垂线).
分析:连接OC,可得△OBD≌△OEC,进而在直角三角形中通过勾股定理建立平衡,得出结论.
点评:熟练掌握全等三角形及勾股定理的性质.

练习册系列答案
相关题目
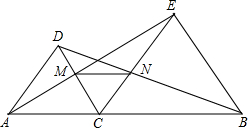 AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N. 已知:如图,点P是等边三角形ABC内一点,
已知:如图,点P是等边三角形ABC内一点, 23、已知:如图,点P是等边△ABC内一点,∠APB=112°,如果把△APB绕点A旋转,使点B与点C重合,此时点P落在点P'处,求∠PP'C的度数.
23、已知:如图,点P是等边△ABC内一点,∠APB=112°,如果把△APB绕点A旋转,使点B与点C重合,此时点P落在点P'处,求∠PP'C的度数. 已知:如图,点P是等边三角形ABC内一点,
已知:如图,点P是等边三角形ABC内一点,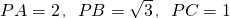 ,求∠BPC的度数.
,求∠BPC的度数. 已知:如图,点P是等边△ABC内一点,∠APB=112°,如果把△APB绕点A旋转,使点B与点C重合,此时点P落在点P'处,求∠PP'C的度数.
已知:如图,点P是等边△ABC内一点,∠APB=112°,如果把△APB绕点A旋转,使点B与点C重合,此时点P落在点P'处,求∠PP'C的度数.