题目内容

已知一等腰三角形的两边长分别是4和6，则它的面积为（  ）
A．　　 B．16
C．6或16D．3或
D

试题分析：题目中没有明确底和腰，故要分情况讨论，先根据等腰三角形的性质结合勾股定理求得高，再根据三角形的面积公式即可求得结果.
若两腰长为4，底边为6，则底边上的高为
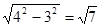
此时三角形的面积；
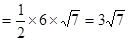若两腰长为6，底边为4，则底边上的高为
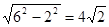
此时三角形的面积；
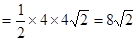故选D.
点评：解答本题的关键是熟练掌握等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．
练习册系列答案
相关题目
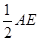如图，在△ABC中，AC=BC，∠ACB=90°，AE平分∠BAC交BC于E，BD⊥AE于D，DM⊥AC交AC的延长线于M，连接CD．下列结论：①BC+CE=AB，②BD=，③BD=CD，④∠ADC=45°，⑤AC+AB=2AM；其中不正确的结论有（    ）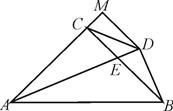

A．0个              B．1个     C．2个             D．3个
在△ABC中，中线AD、BE相交于点O，且S△BOD＝5，则△ABC的面积是（    ）
（A）30；       （B）20；        （C）15；       （D）5．
如图，已知每一个小正方形的边长为1，则△ABC的面积为____________.
已知直角△ABC的周长为6+2，其中一条直角边的长为2，则另一条直角边的长为  ．
已知等腰三角形的两边长分别为6cm，3cm，则这个三角形的周长为      。
如图，OA＝OB，OC＝OD，∠O＝50°，∠D＝30°，则∠AEC等于（   ）
A．70°B．50°C．45°D．60°
如图，在△ABC中，AB=AC，已知AB=17cm，BC=16cm，AD是BC边上中线，则AD的长是   ，△ABC的面积是          ．
一个十二边形的内角和是        度 ，外角和是       度.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网