题目内容
【题目】阅读以下内容,并回答问题:
若一个三角形的两边平方和等于第三边平方的两倍,我们称这样的三角形为奇异三角形.
(1)命题“等边三角形一定是奇异三角形”是 命题(填“真”或“假”);
(2)在△ABC中,已知∠C=90°,△ABC的内角∠A、∠B、∠C所对边的长分别为a、b、c,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
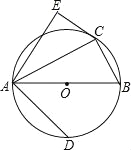
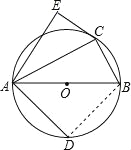
(3)如图,已知AB是⊙O的直径,C是⊙O上一点(点C与点A、B不重合),D是半圆![]() 的中点,C、D在直径AB的两侧,若存在点E,使AE=AD,CB=CE.求证:△ACE是奇异三角形.
的中点,C、D在直径AB的两侧,若存在点E,使AE=AD,CB=CE.求证:△ACE是奇异三角形.
【答案】(1)真(2)![]() (3)证明见解析
(3)证明见解析
【解析】
试题分析:(1)直接根据奇异三角形的定义直接得出结论;
(2)先根据勾股定理得出a2+b2=c2,再由Rt△ABC是奇异三角形,且b>a可知a2+c2=2b2,把a当作已知条件表示出b,c的值,进而可得出结论;
(3)连接BD,根据圆周角定理得出∠ACB=∠ADB=90°,在Rt△ACB与在Rt△ADB中可得出AC2+BC2=AB2,AD2+BD2=AB2,根据点D是半圆![]() 的中点,得出
的中点,得出![]() .故可得出AD=BD.通过等量代换可得出AC2+CB2=2AD2.再由CB=CE,AE=AD可得出AC2+CE2=2AE2故可得出结论.
.故可得出AD=BD.通过等量代换可得出AC2+CB2=2AD2.再由CB=CE,AE=AD可得出AC2+CE2=2AE2故可得出结论.
试题解析:(1)∵若一个三角形的两边平方和等于第三边平方的两倍,我们称这样的三角形为奇异三角形,
∴等边三角形一定是奇异三角形是真命题.
故答案为:真;
(2)∵∠C=90°,
∴a2+b2=c2①.
∵Rt△ABC是奇异三角形,且b>a,
∴a2+c2=2b2②.
由①②得:b=![]() a,c=
a,c=![]() a.
a.
∴a:b:c=![]() .
.
(3)连接BD.
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°.
在Rt△ACB中,AC2+BC2=AB2,
在Rt△ADB中,AD2+BD2=AB2,
∵点D是半圆![]() 的中点,
的中点,
∴![]() .
.
∴AD=BD.
∴AB2=AD2+BD2=2AD2.
∴AC2+CB2=2AD2.
又∵CB=CE,AE=AD,
∴AC2+CE2=2AE2.
∴△ACE是奇异三角形.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案【题目】某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
乙班 | 100 | 95 | 110 | 91 | 104 | 500 |
经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.
请你回答下列问题:
(1)计算两班的优秀率.
(2)计算两班比赛数据的方差.
(3)根据以上信息,你认为应该把冠军奖杯发给哪一个班级?简述你的理由.