题目内容
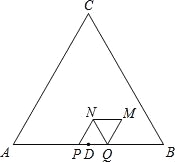
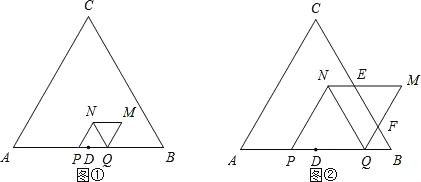
【题目】如图,△ABC是等边三角形,AB=6cm,D为边AB中点.动点P、Q在边AB上同时从点D出发,点P沿D→A以1cm/s的速度向终点A运动.点Q沿D→B→D以2cm/s的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3).
(1)当点N落在边BC上时,求t的值.
(2)当点N到点A、B的距离相等时,求t的值.
(3)当点Q沿D→B运动时,求S与t之间的函数表达式.
(4)设四边形PQMN的边MN、MQ与边BC的交点分别是E、F,直接写出四边形PEMF与四边形PQMN的面积比为2:3时t的值.
【答案】(1)![]() (2)2(3)S=S菱形PQMN=2S△PNQ=
(2)2(3)S=S菱形PQMN=2S△PNQ=![]() t2;
t2;![]() (4)t=1或
(4)t=1或![]()
【解析】
试题分析:(1)由题意知:当点N落在边BC上时,点Q与点B重合,此时DQ=3;
(2)当点N到点A、B的距离相等时,点N在边AB的中线上,此时PD=DQ;
(3)当0≤t≤![]() 时,四边形PQMN与△ABC重叠部分图形为四边形PQMN;当
时,四边形PQMN与△ABC重叠部分图形为四边形PQMN;当![]() ≤t≤
≤t≤![]() 时,四边形PQMN与△ABC重叠部分图形为五边形PQFEN.
时,四边形PQMN与△ABC重叠部分图形为五边形PQFEN.
(4)MN、MQ与边BC的有交点时,此时![]() <t<
<t<![]() ,列出四边形PEMF与四边形PQMN的面积表达式后,即可求出t的值.
,列出四边形PEMF与四边形PQMN的面积表达式后,即可求出t的值.
试题解析:(1)∵△PQN与△ABC都是等边三角形,
∴当点N落在边BC上时,点Q与点B重合.
∴DQ=3
∴2t=3.
∴t=![]() ;
;
(2)∵当点N到点A、B的距离相等时,点N在边AB的中线上,
∴PD=DQ,
当0<t<![]() 时,
时,
此时,PD=t,DQ=2t
∴t=2t
∴t=0(不合题意,舍去),
当![]() ≤t<3时,
≤t<3时,
此时,PD=t,DQ=6﹣2t
∴t=6﹣2t,
解得t=2;
综上所述,当点N到点A、B的距离相等时,t=2;
(3)由题意知:此时,PD=t,DQ=2t
当点M在BC边上时,
∴MN=BQ
∵PQ=MN=3t,BQ=3﹣2t
∴3t=3﹣2t
∴解得t=![]()
如图①,当0≤t≤![]() 时,
时,
S△PNQ=![]() PQ2=
PQ2=![]() t2;
t2;
∴S=S菱形PQMN=2S△PNQ=![]() t2,
t2,
如图②,当![]() ≤t≤
≤t≤![]() 时,
时,
设MN、MQ与边BC的交点分别是E、F,
∵MN=PQ=3t,NE=BQ=3﹣2t,
∴ME=MN﹣NE=PQ﹣BQ=5t﹣3,
∵△EMF是等边三角形,
∴S△EMF=ME2=
![]() (5t﹣3)2
(5t﹣3)2
![]() .
.
![]() ;
;
(4)MN、MQ与边BC的交点分别是E、F,
此时![]() <t<
<t<![]() ,
,
t=1或![]() .
.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案