题目内容
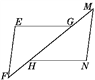
【题目】如图所示,已知BE平分∠ABC,∠1=∠2,求证:∠AED=∠C.完善以下推理过程. 证明:∵BE平分∠ABC,∴∠1=∠3. ()
又∵∠1=∠2(已知),∴=( 等量代换),
∴∥()
∴∠AED=∠C ().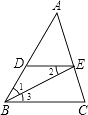
【答案】已知;∠2;∠3;DE;BC;内错角相等,两直线平行;两直线平行,同位角相等
【解析】证明:∵BE平分∠ABC, ∴∠1=∠3(角平分线定义),
又∵∠1=∠2(已知),
∴∠2=∠3(等量代换),
∴DE∥BC(内错角相等,两直线平行),
∴∠AED=∠C(两直线平行,同位角相等).
故答案为:已知,∠2,∠3,DE,BC,内错角相等,两直线平行,两直线平行,同位角相等.
先根据等量代换,得出∠2=∠3,再根据平行线的判定,得出DE∥BC,最后根据平行线的性质,得出∠AED=∠C.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目