题目内容
【题目】教材中,在计算如图1所示的正方形ABCD的面积时,分别从两个不同的角度进行了操作: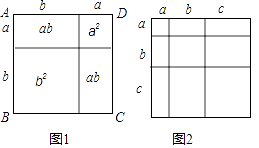
(i)把它看成是一个大正方形,则它的面积为(a+b)2;
(ii)把它看成是2个小长方形和2个小正方形组成的,则它的面积为a2+2ab+b2;因此,可得到等式:(a+b)2=a2+2ab+b2 .
(1)类比教材中的方法,由图2中的大正方形可得等式: .
(2)试在图2右边空白处画出面积为2a2+3ab+b2的长方形的示意图(标注好a,b) ,由图形可知,多项式2a2+3ab+b2可分解因式为: .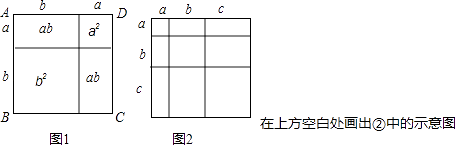
(3)若将代数式(a1+a2+a3+…+a20)2展开后合并同类项,得到多项式N,则多项式N的项数一共有项.
【答案】
(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
(2)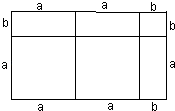 ;2a2+3ab+b2=(2a+b)(a+b)
;2a2+3ab+b2=(2a+b)(a+b)
(3)210
【解析】解:(1.)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
所以答案是:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2.)如图,
2a2+3ab+b2=(2a+b)(a+b),
所以答案是:2a2+3ab+b2=(2a+b)(a+b);
(3.)∵(a1+a2)2=a12+2a1a2+a22 , 共有2+1=3项;
(a1+a2+a3)2=a12+a22+a32+2a1a2+2a2a3+2a3a3 , 共有1+2+3=6项,
…
∴(a1+a2+a3+…+a20)2展开后合并同类项共有1+2+3+…+20= ![]() =210项,
=210项,
所以答案是:210.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目