题目内容
甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:
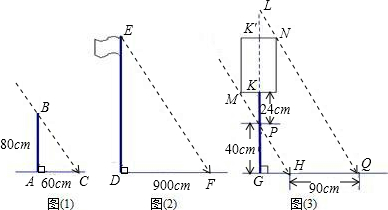
甲组:如图(1),测得一根直立于平地,长为80cm的竹竿的影长为60cm.
乙组:如图(2),测得学校旗杆的影长为900cm.
丙组:如图(3),测得校园景灯(灯罩视为圆柱体,灯杆粗细忽略不计)的灯罩部分影长HQ为90cm,灯杆被阳光照射到的部分PG长40cm,未被照射到的部分KP长24cm.
(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;
(2)请根据甲、丙两组得到的信息,求:
①灯罩底面半径MK的长;
②灯罩的主视图面积.
解:(1)因为在同一时刻在阳光下对校园中,学校旗杆与旗杆的影长构成直角三角形Rt△ABC和Rt△DEF,且Rt△ABC∽Rt△DEF,
所以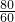 =
=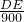 ,
,
所以DE=1200cm;
(2)①由(1)可知Rt△PGH∽Rt△PKM∽Rt△ABC,得出GH=30cm,MK=18cm
②Rt△PKM≌Rt△LK′N,由KP长24cm,得出LK′=24cm,Rt△ABC∽Rt△LGQ,
所以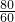 =
=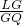 =
=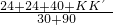 ,
,
所以KK'=72cm,
灯罩的主视图面积为:18×2×72=2592cm2.
分析:(1)根据在同一时刻在阳光下对校园中,学校旗杆与旗杆的影长构成直角三角形Rt△ABC和Rt△DEF相似进行解答即可;
(2)①根据(1)可知Rt△PGH∽Rt△PKM∽Rt△ABC,再根据相似三角形的对应边成比例进行解答;
②先根据相似三角形的判定定理得出Rt△PKM≌Rt△LK′N,Rt△ABC∽Rt△LGQ,再根据相似三角形的性质进行解答即可.
点评:本题考查的是相似三角形在实际生活中的运用,解答此类题目的关键是根据相似三角形的判定定理得出相似的三角形,再根据相似三角形的性质解答.
所以
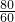 =
=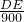 ,
,所以DE=1200cm;
(2)①由(1)可知Rt△PGH∽Rt△PKM∽Rt△ABC,得出GH=30cm,MK=18cm
②Rt△PKM≌Rt△LK′N,由KP长24cm,得出LK′=24cm,Rt△ABC∽Rt△LGQ,
所以
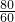 =
=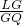 =
=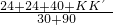 ,
,所以KK'=72cm,
灯罩的主视图面积为:18×2×72=2592cm2.
分析:(1)根据在同一时刻在阳光下对校园中,学校旗杆与旗杆的影长构成直角三角形Rt△ABC和Rt△DEF相似进行解答即可;
(2)①根据(1)可知Rt△PGH∽Rt△PKM∽Rt△ABC,再根据相似三角形的对应边成比例进行解答;
②先根据相似三角形的判定定理得出Rt△PKM≌Rt△LK′N,Rt△ABC∽Rt△LGQ,再根据相似三角形的性质进行解答即可.
点评:本题考查的是相似三角形在实际生活中的运用,解答此类题目的关键是根据相似三角形的判定定理得出相似的三角形,再根据相似三角形的性质解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



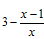 的值随着x 的增大越来越小;
的值随着x 的增大越来越小; 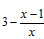 的值有可能等于2;
的值有可能等于2;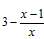 的值随着x 的增大越来越接近于2。
的值随着x 的增大越来越接近于2。