Question

某校九（2）班学生在一次活动课中，甲、乙、丙三个学习小组于同一时刻在阳
光下对校园中一些物体进行了测量，下面是他们通过测量得到的一些信息：
甲组：如图1，测得一根直立于平地，长为80cm的竹竿的影长为60cm，
乙组：如图2，测得学校旗杆的影长为900 cm，
丙组：如图3，测得校园景灯（灯罩视为球体，灯杆为圆柱体，其粗细忽略不计）的高度为200 cm，影长为156 cm.
请你根据以上信息，解答下列问题：
【小题1】计算学校旗杆的高度.
【小题2】如图3，设太阳光线NH与⊙O相切于点M，请根据甲、丙两组得到的信息，求景灯灯罩的半径.（友情提示：如图3，景灯的影长等于线段NG的影长，需要时可采用等式156²+208²=260²）

Answer 1

【小题1】由题意可知：∠BAC=∠EDF=90° ∠BCA=∠EFD  ∴△ABC∽△DEF
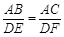∴ 即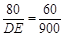  ∴DE=1200（cm）
∴学校旗杆的高度是12 cm
【小题1】与（1）类似得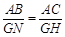：  即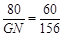  ∴GN=208
在Rt△NGH中，根据勾股定理得：NH²=156²+208²=260²   ∴NH=260
设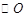的半径为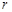cm，连OM，∵NH切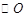于M   ∴OM⊥NH
则∠OMN=∠HGN=90° 又∠ONM=∠HNG  ∴△OMN∽△HGN
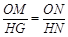∴  又
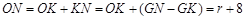
∴  解得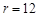  ∴景灯灯罩的半径是12 cm.

解析【小题1】根据同一时刻物高与影长成正比即可求出旗杆的高度；
【小题1】先根据同一时刻物高与影长成正比求出NG的长，再连接OM，由切线的性质可知OM⊥NH，进而可得出△NMO∽△NGH，再根据其对应边成比例列出比例式，然后用半径表示出ON，进行计算即可求出OM的长