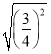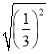题目内容
【题目】如图,长方体的长为15厘米,宽为10厘米,高为20厘米,点B到点C的距离是5厘米.
(1)通过计算,一只小虫在长方体表面从A爬到B的最短路程是多少?
(2)在此长方体盒子内放入一根木棒,木棒的最大长度是多少?

【答案】(1)25厘米;(2)![]() 厘米
厘米
【解析】
(1)求长方体中两点之间的最短路径,最直接的作法,就是将长方体侧面展开,然后利用两点之间线段最短解答.
(2)利用长方体的性质,根据勾股定理解答即可.
解:(1)把长方体的右侧表面展开与前面这个侧面所在的平面形成一个长方形,如图1:
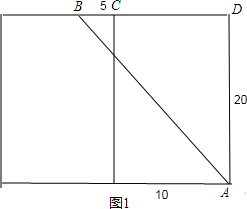
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5,
∴BD=CD+BC=10+5=15cm,AD=20cm,
在直角三角形ABD中,根据勾股定理得:
∴AB=![]() =
=![]() =25cm;
=25cm;
把长方体的右侧表面展开与上面这个侧面所在的平面形成一个长方形,如图2:
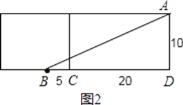
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5,
∴BD=CD+BC=20+5=25cm,AD=10cm,
在直角三角形ABD中,根据勾股定理得:
∴AB=![]() =
=![]() =5
=5![]() cm;
cm;
把长方体的上面表面展开与后面这个侧面所在的平面形成一个长方形,如图3:
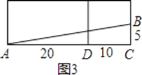
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴AC=CD+AD=20+10=30cm,
在直角三角形ABC中,根据勾股定理得:
∴AB=![]() =
=![]() =5
=5![]() cm;
cm;
∵25<5![]() <5
<5![]() ,
,
∴自A至B在长方体表面的连线距离最短是25cm.
故答案为:25厘米;
(2)连接AE,EG,
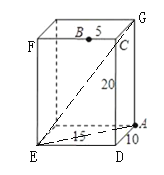
在Rt△ADE中,AD=10cm,ED=15cm,由勾股定理得,
AE=![]() =
=![]() =5
=5![]() cm,
cm,
在Rt△AEG中,AE=5![]() cm,AG=20cm,
cm,AG=20cm,
由勾股定理得,EG=![]() =
=![]() =5
=5![]() cm.
cm.
即木棒的最大长度是5![]() 厘米.
厘米.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目