Question

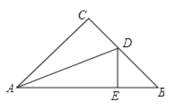
【题目】如图所示，在菱形ABCD中，∠B＝∠EAF＝60°，∠BAE＝20°，则∠AEF的大小是_____．

Answer 1

【答案】60°

【解析】

由菱形的性质可证△ABC，△ACD都是等边三角形，可得∠B＝∠ACF＝∠BAC＝60°，则可证△ABE≌△ACF，可得AE＝AF，即可证△AEF是等边三角形，即可求∠AEF的大小．

解：连接AC

∵四边形ABCD是菱形

∴AB＝BC＝CD＝AD，∠B＝∠D＝60°

∴△ABC，△ACD都是等边三角形

∴AC＝AB，∠B＝∠ACD＝60°＝∠BAC

∵∠BAC＝60°＝∠EAF

∴∠BAE＝∠CAF

又∵AC＝AB，∠B＝∠ACD＝60°

∴△ABE≌△ACF

′∴AE＝AF且∠EAF＝60°

∴△AEF是等边三角形

∴∠AEF＝60°

故答案为60°