Question

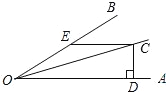
【题目】如图，在矩形纸片ABCD中，AB=3，BC=9．将矩形纸片折叠，使点B和点D重合．

（1）求ED的长；

（2）求折痕EF的长．

Answer 1

【答案】（1）5；（2）

【解析】

（1）先依据翻折的性质和平行线的性质证明三角形DEF为等腰三角形，从而得到ED=DF，设DE=x，则DF=x，FC=9-x，然后在△DFC中依据勾股定理列方程求解即可；
（2）过点E做EM垂直于BC，垂足为M．先求得MF的长度，然后依据勾股定理可求得EF的长．

解：（1）∵四边形ABCD为矩形，

∴AB=CD=3．

∵AD∥BC，

∴∠BFE=∠DEF．

∵∠BFE=∠EFD，

∴∠EFD=∠DEF，

∴DE=DF．

设DE=x，则DF=x，FC=9﹣x．

在Rt△DFC中，FC2+DC2=DF2，

∴（9﹣x）2+32=x2．解得x=5．

∴DE=5．

（2）过点E做EM垂直于BC，垂足为M．

根据（1）可知BF=DF=5,

AE=CF=4，

∵AE=CF=4，BF=DF=5，

∴MF=BF﹣BM=5﹣4=1．

∴Rt△MEF中，EF2=EM2+MF2=32+12=10

∴