题目内容
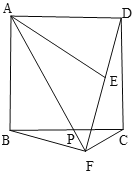
【题目】如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列四个结论:①AC=AD;② AB⊥EB;③BC=EC;④∠A=∠EBC;其中一定正确的是( )

A.②B.②③C.③④D.②③④
【答案】C
【解析】
根据旋转的性质得到BC=CE ,AC=CD,AB=DE,故![]() 错误,
错误,![]() 正确;得到∠ACD=∠BCE,根据三角形的内角和得到∠A=∠ADC=
正确;得到∠ACD=∠BCE,根据三角形的内角和得到∠A=∠ADC=![]() ,∠CBE=
,∠CBE=![]() ,求得∠A=∠EBC,故
,求得∠A=∠EBC,故![]() 正确;由于∠A+∠ABC不一定等于90°,可以得到∠ABC+∠CBE不一定等于90°,故
正确;由于∠A+∠ABC不一定等于90°,可以得到∠ABC+∠CBE不一定等于90°,故![]() 错误.
错误.
解:∵△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD,BC=CE,AB=DE,故![]() 错误,
错误,![]() 正确;
正确;
∴∠ACD=∠BCE,
∴![]()
∴∠A=∠EBC,故![]() 正确
正确
∵∠A+∠ABC不一定等于90°
∴∠ABC+∠CBE不一定等于90°,故![]() 错误
错误
故选 C

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
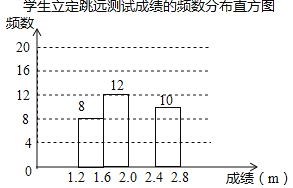
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?