题目内容

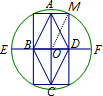
如图，顺次连接圆内接矩形各边的中点，得到菱形ABCD，若BD=6，DF=4，则菱形ABCD的边长为（　　）
A．4
2
B．3
2
C．5D．7

连接OM，
∵BD=6，DF=4，
∴OD=3，OF=OM=3+4=7，
由勾股定理得：OA=MD=
OM2-OD2
=2
10
，
∵菱形ABCD，
∴AC⊥BD，
由勾股定理得：AD=
OA2+OD2
=
32+(2
10
)2
=7．
故选D．
练习册系列答案
相关题目
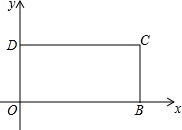如图所示，在直角坐标系中，矩形OBCD的边长OB=4，OD=2，点P是射线OB上一个动点，动点Q在PB或其延长线上运动，OP=PQ，作以PQ为一边的正方形PQRS，点P从O点开始沿射线OB方向运动，运动速度是1个单位/秒，运动时间为t秒，直到点P与点B重合为止．
（1）设正方形PQRS与矩形OBCD重叠部分的面积为y，写出y与t的函数关系式；
（2）y=2时，求t的值；
（3）当t为何值时，三角形CSR为等腰三角形？
将一长方形切去一角后得一边长分别为13、19、20、25和31的五边形（顺序不一定按此），则此五边形的面积为（　　）
A．680B．720C．745D．760
如图，在等边△ABC中，点D是BC边的中点，以AD为边作等边△ADE．
（1）求∠CAE的度数；
（2）取AB边的中点F，连接CF、CE，试证明四边形AFCE是矩形．
如图，扇形OAB的半径OA=3，圆心角∠AOB=90°，点C是
AB
上异于A、B的动点，过点C作CD⊥OA于点D，作CE⊥OB于点E，连接DE，点G、H在线段DE上，且DG=GH=HE
（1）求证：四边形OGCH是平行四边形；
（2）当点C在
AB
上运动时，在CD、CG、DG中，是否存在长度不变的线段？若存在，请求出该线段的长度；
（3）求证：CD2+3CH2是定值．
如图，四边形ABCD是平行四边形，对角线AC、BD交于点O，∠OBC=∠OCB，求证：四边形ABCD是矩形．
矩形ABCD中，横向阴影部分是长方形，另一部分是平行四边形，依照图中标注的数据，图中空白部分的面积为（　　）
A．bc-ab+ac+c2B．ab-bc-ac+c2
C．a2+ab+bc-acD．b2-bc+a2-ab
如图，在菱形ABCD中，∠ABC与∠BAD的度数比为1：2，周长是48cm．求：
（1）两条对角线的长度；
（2）菱形的面积．
如图，菱形ABCD的边长为8cm，∠A=60°，DE⊥AB于点E，DF⊥BC于点F，则四边形BEDF的面积为______cm2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网