ĢāÄæÄŚČŻ
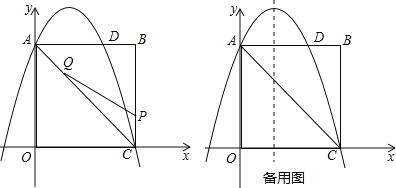
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy£½©ax2+2ax+cÓėxÖįĻą½»ÓŚA£Ø©1£¬0£©”¢BĮ½µć£ØAµćŌŚBµć×ó²ą£©£¬ÓėyÖįĻą½»ÓŚµćC£Ø0£¬3![]() £©£¬µćDŹĒÅ×ĪļĻߵĶ„µć£®
£©£¬µćDŹĒÅ×ĪļĻߵĶ„µć£®
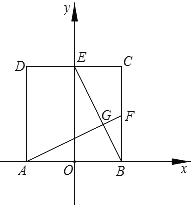
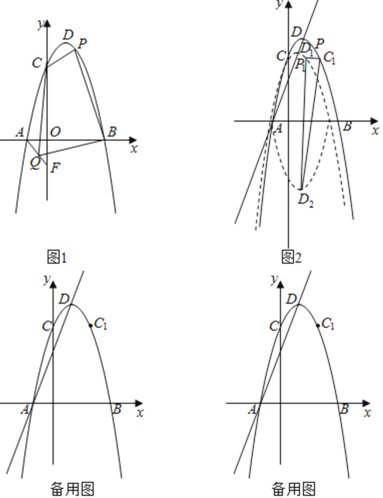
£Ø1£©ČēĶ¼1£¬ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ČēĶ¼1£¬µćF£Ø0£¬b£©ŌŚyÖįÉĻ£¬Į¬½ÓAF£¬µćQŹĒĻ߶ĪAFÉĻµÄŅ»øö¶Æµć£¬PŹĒµŚŅ»ĻóĻŽÅ×ĪļĻßÉĻµÄŅ»øö¶Æµć£¬µ±b£½©![]() Ź±£¬ĒóĖıߊĪCQBPĆ껿µÄ×ī“óÖµÓėµćPµÄ×ų±ź£»
Ź±£¬ĒóĖıߊĪCQBPĆ껿µÄ×ī“óÖµÓėµćPµÄ×ų±ź£»
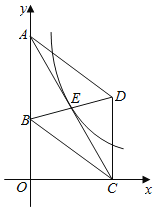
£Ø3£©ČēĶ¼2£¬µćC1ÓėµćC¹ŲÓŚÅ×ĪļĻ߶Ō³ĘÖį¶Ō³Ę£®½«Å×ĪļĻßyŃŲÖ±ĻßADĘ½ŅĘ£¬Ę½ŅĘŗóµÄÅ×ĪļĻß¼ĒĪŖy1£¬y1µÄ¶„µćĪŖD1£¬½«Å×ĪļĻßy1ŃŲxÖį·ÕŪ£¬·ÕŪŗóµÄÅ×ĪļĻß¼ĒĪŖy2£¬y2µÄ¶„µćĪŖD2£®ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬µćPĘ½ŅĘŗóµÄ¶ŌÓ¦µćĪŖP1£¬ŌŚĘ½ŅĘ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚŅŌP1D2ĪŖŃüµÄµČŃü”÷C1P1D2£¬Čō“ęŌŚĒėÖ±½ÓŠ“³öµćD2µÄŗį×ų±ź£¬Čō²»“ęŌŚĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©y£½©![]() x2+2
x2+2![]() x+3
x+3![]() £»£Ø2£©µ±m£½
£»£Ø2£©µ±m£½![]() Ź±£¬SĖıߊĪCQBPČ”µĆ×ī“óÖµ
Ź±£¬SĖıߊĪCQBPČ”µĆ×ī“óÖµ![]() £¬“ĖŹ±Pµć×ų±źĪŖ£Ø
£¬“ĖŹ±Pµć×ų±źĪŖ£Ø![]() £¬
£¬![]() £©£»£Ø3£©“ęŌŚ£¬Āś×ćŅŖĒóµÄD2µÄŗį×ų±źÓŠ£ŗ
£©£»£Ø3£©“ęŌŚ£¬Āś×ćŅŖĒóµÄD2µÄŗį×ų±źÓŠ£ŗ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £®
£®
”¾½āĪö”æ
£Ø1£©½«A”¢CĮ½µć×ų±ź“śČėÅ×ĪļĻß½āĪöŹ½µ±ÖŠĒó³öaÓėcµÄÖµ¼“æÉ£»
£Ø2£©ĻČĒó³öB”¢F×ų±ź£¬Č»ŗóæÉŅŌÖ¤Ć÷AFÓėBCĘ½ŠŠ£¬ÓŚŹĒ”÷QBCµÄĆ껿¾ĶµČÓŚ”÷ABCµÄĆ껿£¬ĪŹĢā¾Ķ×Ŗ»ÆĪŖĒó”÷PBCµÄĆ껿µÄ×ī“óÖµ£¬×÷PE”ĪyÖį½»Ö±ĻßBCÓŚE£¬ÉčPµćµÄŗį×ų±źĪŖĪ“ÖŖŹżm£¬½«Eµć×ų±źŅ²ÓĆm±ķŹ¾£¬PEµÄ³¤¶ČÓĆP”¢Eׯ×ų±źÖ®²ī±ķŹ¾£¬ÓŚŹĒ”÷PBCµÄĆ껿¾ĶæÉŅŌ±ķŹ¾³É¹ŲÓŚmµÄ¶ž“ĪŗÆŹż£¬ĶعżÅä·½·Ø¼“æÉĒó³ö×īÖµ¼°Pµć×ų±ź£®
£Ø3£©ÓÉÓŚĻŽ¶ØĮĖŅŌP1D2ĪŖŃü£¬Ņņ“Ė·ÖĮ½“óĄą·Ö±šĮŠ·½³Ģ¼ĘĖć¼“æÉ£®
£Ø1£©½«A£Ø©1£¬0£©”¢C£Ø0£¬3![]() £©“śČėÅ×ĪļĻß½āĪöŹ½µĆ£ŗ
£©“śČėÅ×ĪļĻß½āĪöŹ½µĆ£ŗ
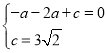
½āµĆ£ŗ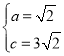 £¬
£¬
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy£½©![]() x2+2
x2+2![]() x+3
x+3![]() £®
£®
£Ø2£©ČēĶ¼1£¬Į¬½ÓBC£¬AC£¬×÷PE”ĪyÖį½»BCÓŚE£®
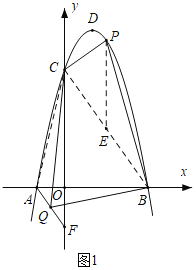
”ßy£½©![]() x2+2
x2+2![]() x+3
x+3![]() £½©
£½©![]() £Øx+1£©£Øx©3£©£®
£Øx+1£©£Øx©3£©£®
”ąB£Ø3£¬0£©£¬
”ßb£½©![]() £¬
£¬
”ąF£Ø0£¬©![]() £©£¬
£©£¬
”ą![]() £½
£½![]() £¬
£¬
”ąAF”ĪBC£¬
”ąS”÷QBC£½S”÷ABC£½![]() ABOC£½6
ABOC£½6![]() £¬
£¬
ÓÉB”¢CĮ½µć×ų±źæɵĆÖ±ĻßBCµÄ½āĪöŹ½ĪŖ£ŗy£½©![]() x+3
x+3![]() £¬
£¬
ÉčP£Øm£¬©![]() m2+2
m2+2![]() m+3
m+3![]() £©£¬ŌņE£Øm£¬©
£©£¬ŌņE£Øm£¬©![]() m+3
m+3![]() £©£¬
£©£¬
PE£½yP©yE£½©![]() m2+4
m2+4![]() m£¬
m£¬
”ąS”÷PBC£½![]() £ØxB©xC£©£ØyP©yE£©£½©
£ØxB©xC£©£ØyP©yE£©£½©![]() m2+6
m2+6![]() m£½©
m£½©![]() £Øm©
£Øm©![]() £©2+
£©2+![]() £¬
£¬
”ąSĖıߊĪCQBP£½S”÷QBC+S”÷PBC£½S”÷ABC+S”÷PBC£½©![]() £Øm©
£Øm©![]() £©2+
£©2+![]() £¬
£¬
”ąµ±m£½![]() Ź±£¬SĖıߊĪCQBPČ”µĆ×ī“óÖµ
Ź±£¬SĖıߊĪCQBPČ”µĆ×ī“óÖµ![]() £¬“ĖŹ±Pµć×ų±źĪŖ£Ø
£¬“ĖŹ±Pµć×ų±źĪŖ£Ø![]() £¬
£¬![]() £©£®
£©£®
£Ø3£©”ßy£½©![]() x2+2
x2+2![]() x+3
x+3![]() £½
£½![]() £¬
£¬
”ąD£Ø1£¬4![]() £©£¬Å×ĪļĻ߶Ō³ĘÖįĪŖx£½1£¬
£©£¬Å×ĪļĻ߶Ō³ĘÖįĪŖx£½1£¬
”ßC1ÓėC¹ŲÓŚÖ±Ļßx£½1¶Ō³Ę£¬
”ąC1£Ø2£¬3![]() £©£¬
£©£¬
ÓÉA”¢DĮ½µć×ų±źæÉĒóµĆÖ±ĻßADµÄ½āĪöŹ½ĪŖy£½2![]() x+2
x+2![]() £¬
£¬
ÉčD1£Øm£¬2![]() m+2
m+2![]() £©£¬
£©£¬
ŌņP1£Øm+![]() £¬2
£¬2![]() m+
m+![]() £©£¬D2£Øm£¬©2
£©£¬D2£Øm£¬©2![]() m©2
m©2![]() £©£¬
£©£¬
”ą![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬
µ±P1C1£½P1D2Ź±£¬![]() £½
£½![]() £¬½āµĆ
£¬½āµĆ![]() £¬
£¬![]() £®
£®
µ±C1D2£½P1D2Ź±£¬9m2+36m+54£½![]() £¬½āµĆ
£¬½āµĆ![]() £¬
£¬![]() £®
£®
×ŪÉĻĖłŹö£¬Āś×ćŅŖĒóµÄD2µÄŗį×ų±źÓŠ£ŗ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £®
£®

”¾ĢāÄæ”æ2020Äź×¢¶ØŹĒ²»Ę½·²µÄŅ»Äź£¬ŠĀÄźŅĮŹ¼£¬Ņ»³”Ķ»ČēĘ䥓µÄŅßĒéĻƾķČ«¹ś£¬Č«¹śČĖĆńĶņÖŚŅ»ŠÄ£¬æ¹Õ½ŅßĒ飮ĪŖĮĖŌēČÕČ”µĆæ¹Ņߵ拉ū£¬ø÷¼¶Õžø®”¢ø÷“óŠĀĪÅĆ½Ģ嶼¼Ó“óĮĖ¶Ō·ĄŅßÖŖŹ¶µÄŠū“«£®Ä³Š£ĪŖĮĖĮĖ½ā³õŅ»Äź¼¶¹²480ĆūĶ¬Ń§¶Ō·ĄŅßÖŖŹ¶µÄÕĘĪÕĒéæö£¬¶ŌĖūĆĒ½ųŠŠĮĖ·ĄŅßÖŖŹ¶²āŹŌ£®ĻÖĖ껜³éČ”¼×”¢ŅŅĮ½°ąø÷15ĆūĶ¬Ń§µÄ²āŹŌ³É¼Ø£ØĀś·Ö100·Ö£©½ųŠŠÕūĄķ·ÖĪö£¬¹ż³ĢČēĻĀ£ŗ
£ØŹÕ¼ÆŹż¾Ż£©
¼×°ą15Ćūѧɜ²āŹŌ³É¼Ø·Ö±šĪŖ£ŗ78£¬83£¬89£¬97£¬98£¬85£¬100£¬94£¬87£¬90£¬93£¬92£¬99£¬95£»100£®
ŅŅ°ą15Ćūѧɜ²āŹŌ³É¼ØÖŠ90”Üx£¼95µÄ³É¼ØČēĻĀ£ŗ91£¬92£¬94£¬90£¬93
£ØÕūĄķŹż¾Ż£©£ŗ
°ą¼¶ | 75”Üx£¼80 | 80”Üx£¼85 | 85”Üx£¼90 | 90”Üx£¼95 | 95”Üx£¼100 |
¼× | 1 | 1 | 3 | 4 | 6 |
ŅŅ | 1 | 2 | 3 | 5 | 4 |
£Ø·ÖĪöŹż¾Ż£©£ŗ
°ą¼¶ | Ę½¾łŹż | ÖŚŹż | ÖŠĪ»Źż | ·½²ī |
¼× | 92 | a | 93 | 47.3 |
ŅŅ | 90 | 87 | b | 50.2 |
£ØÓ¦ÓĆŹż¾Ż£©£ŗ
£Ø1£©øł¾ŻŅŌÉĻŠÅĻ¢£¬æÉŅŌĒó³ö£ŗa£½_____·Ö£¬b£½______·Ö£»
£Ø2£©Čō¹ę¶Ø²āŹŌ³É¼Ø92·Ö¼°ĘäŅŌÉĻĪŖÓÅŠć£¬Ēė¹Ą¼Ę²Ī¼Ó·ĄŅßÖŖŹ¶²āŹŌµÄ480Ćūѧɜ֊³É¼ØĪŖÓÅŠćµÄѧɜ¹²ÓŠ¶ąÉŁČĖ£»
£Ø3£©øł¾ŻŅŌÉĻŹż¾Ż£¬ÄćČĻĪŖÄÄøö°ąµÄѧɜ·ĄŅß²āŹŌµÄÕūĢå³É¼Ø½ĻŗĆ£æĒėĖµĆ÷ĄķÓÉ£ØŅ»ĢõĄķÓɼ“æÉ£©£®