题目内容
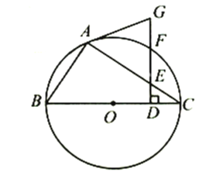
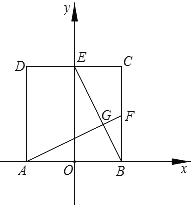
【题目】如图,在正方形ABCD中,顶点A(﹣1,0),C(1,2),点F是BC的中点,CD与y轴交于点E,AF与BE交于点G.将正方形ABCD绕点O顺时针旋转,每次旋转90°,则第99次旋转结束时,点G的坐标为( )
A.(![]() ,
,![]() )B.(﹣
)B.(﹣![]() ,
,![]() )C.(﹣
)C.(﹣![]() ,
,![]() )D.(
)D.(![]() ,﹣
,﹣![]() )
)
【答案】B
【解析】
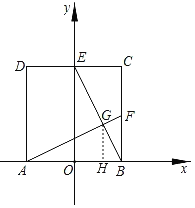
根据正方形的性质得到AB=BC=CD=2,∠C=∠ABF=90°,根据全等三角形的性质得到∠BAF=∠CBE,根据余角的性质得到∠BGF=90°,过G作GH⊥AB于H,根据相似三角形的性质得到BH=![]() =
=![]() ,求得OH=
,求得OH=![]() ,根据勾股定理得到HG=
,根据勾股定理得到HG=![]() =
=![]() ,求得G(
,求得G(![]() ,
,![]() ),找出规律即可得到结论.
),找出规律即可得到结论.
∵四边形ABCD是正方形,
∴AB=BC=CD=2,∠C=∠ABF=90°,
∵点F是BC的中点,CD与y轴交于点E,
∴CE=BF=1,
∴△ABF≌△BCE(SAS),
∴∠BAF=∠CBE,
∵∠BAF+∠BFA=90°,
∴∠FBG+∠BFG=90°,
∴∠BGF=90°,
∴BE⊥AF,
∵AF=![]() =
=![]() =
=![]() ,
,
∴BG=![]() =
=![]() ,
,
过G作GH⊥AB于H,
∴∠BHG=∠AGB=90°,
∵∠HBG=∠ABG,
∴△ABG∽△GBH,
∴![]() ,
,
∴BG2=BHAB,
∴BH=![]() =
=![]() ,
,
∴OH=![]() ,
,
∵OG=![]() AB=1,
AB=1,
∴HG=![]() =
=![]() ,
,
∴G(![]() ,
,![]() ),
),
∵将正方形ABCD绕点O顺时针每次旋转90°,
∴第一次旋转90°后对应的G点的坐标为(![]() ,﹣
,﹣![]() ),
),
第二次旋转90°后对应的G点的坐标为(﹣![]() ,﹣
,﹣![]() ),
),
第三次旋转90°后对应的G点的坐标为(﹣![]() ,
,![]() ),
),
第四次旋转90°后对应的G点的坐标为(![]() ,
,![]() ),
),
…,
∵99=4×24+3,
∴每4次一个循环,第99次旋转结束时,相当于正方形ABCD绕点O顺时针旋转3次,
∴第99次旋转结束时,点G的坐标为(﹣![]() ,
,![]() ).
).
故选:B.

【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?
【题目】某商场销售A、B两种型号的电风扇,进价及售价如表:
品牌 | A | B |
进价(元/台) | 120 | 180 |
售价(元/台) | 150 | 240 |
(1)该商场4月份用21000元购进A、B两种型号的电风扇,全部售完后获利6000元,求商场4月份购进A、B两种型号电风扇的数量;
(2)该商场5月份计划用不超过42000元购进A、B两种型号电风扇共300台,且B种型号的电风扇不少于50台;销售时准备A种型号的电风扇价格不变,B种型号的电风扇打9折销售.那么商场如何进货才能使利润最大?