��Ŀ����
����Ŀ����֪��ABC�ǵ���ֱ�������Σ�AC=BC=2��D�DZ�AB��һ���㣨A��B������⣩������CAD�Ƶ�C����ʱ�뷽����ת�Ǧ��õ���CEF�����е�E�ǵ�A�Ķ�Ӧ�㣬��F�ǵ�D�Ķ�Ӧ�㣮
��1����ͼ1������=90��ʱ��G�DZ�AB��һ�㣬��BG=AD������GF����֤��GF��AC��
��2����ͼ2����90��ܦ���180��ʱ��AE��DF�ཻ�ڵ�M��
�ٵ���M���C��D���غ�ʱ������CM�����CMD�Ķ�����
����DΪ��AB���е㣬������90��仯��180��ʱ�����M�˶���·������
���𰸡�
��1��
֤������ͼ1��
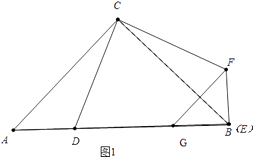 ��
��
��CA=CB����ACB=90�㣬
���A=��ABC=45�㣬
�ߡ�CEF���ɡ�CAD��ת��ʱ����õ�����=90�㣬
��CB��CE�غϣ�
���CBE=��A=45�㣬
���ABF=��ABC+��CBF=90�㣬
��BG=AD=BF��
���BGF=��BFG=45�㣬
���A=��BGF=45�㣬
��GF��AC��
��2��
�⣺����ͼ2��
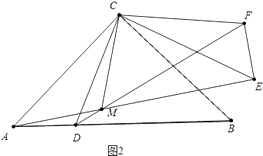 ��
��
��CA=CE��CD=CF��
���CAE=��CEA����CDF=��CFD��
�ߡ�ACD=��ECF��
���ACE=��CDF��
��2��CAE+��ACE=180�㣬2��CDF+��DCF=180�㣬
���CAE=��CDF��
��A��D��M��C�ĵ㹲Բ��
���CMF=��CAD=45�㣬
���CMD=180�㩁��CMF=135�㣮
����ͼ3��
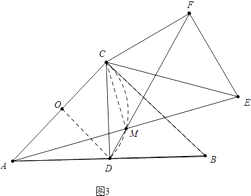 ��
��
O��AC�е㣬����OD��CM��
��AD=DB��CA=CB��
��CD��AB��
���ADC=90�㣬
�ɢٿ�֪A��D��M��C�ĵ㹲Բ��
�൱����90��仯��180��ʱ��
��M����ACΪֱ���ġ�O�ϣ��˶�·���ǻ�CD��
��OA=OC��CD=DA��
��DO��AC��
���DOC=90�㣬
�� ![]() �ij�=
�ij�= ![]() ��
��
�൱����90��仯��180��ʱ����M�˶���·����Ϊ ![]() ��
��
����������1����֤��GF��AC��ֻҪ֤����A=��FGB���ɽ�����⣮��2������֤��A��D��M��C�ĵ㹲Բ���õ���CMF=��CAD=45�㣬���ɽ�����⣮�����âٵĽ��ۿ�֪����M����ACΪֱ���ġ�O�ϣ��˶�·���ǻ�CD�����û�����ʽ���ɽ�����⣮���⿼�鼸�α任�ۺ��⡢����ֱ�������ε����ʡ�ƽ���ߵ��ж������ʡ�������ʽ���ĵ㹲Բ��֪ʶ������Ĺؼ��Ƿ���A��D��M��C�ĵ㹲Բ�����һ������Ĺؼ�����ȷ̽������M���˶�·������ס������ʽ�������п�ѹ���⣮
�����㾫����������Ĺؼ������������ֱ�������ε����֪ʶ�����յ���ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣮









