��Ŀ����
����Ŀ����֪��һ�κ���y=3x��2��ͼ����ij������������ͼ���һ��������ĺ�����Ϊ1��
��1����÷����������Ľ���ʽ��
��2����һ�κ���y=3x��2��ͼ������ƽ��4����λ����ƽ�ƺ��ͼ���뷴��������ͼ��Ľ������ꣻ
��3����ֱ��д��һ��ͬʱ�������������ĺ�������ʽ�� �ٺ�����ͼ������һ�κ���y=3x��2��ͼ���Ƶ㣨0����2����תһ���Ƕȵõ���
�ں�����ͼ���뷴����������ͼ��û�й����㣮
���𰸡�
��1���⣺��x=1����y=3x��2����y=1��
�跴���������Ľ���ʽΪ ![]() ��
��
��x=1��y=1����ã�k=1��
��÷����������Ľ���ʽΪ ![]()
��2���⣺ƽ�ƺ��ͼ���Ӧ�Ľ���ʽΪy=3x+2��
�ⷽ���� 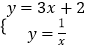 ����
���� ![]() ��
�� ![]() ��
��
��ƽ�ƺ��ͼ���뷴��������ͼ��Ľ�������Ϊ�� ![]() ��3���ͣ���1����1��
��3���ͣ���1����1��
��3���⣺y=��2x��2��
�����ۿ��ţ�������Ϊ��2��һ����ϵ��С�ک�1��һ�κ������ɣ�
����������1��������������Ľ������꣬���ô���ϵ����������÷����������Ľ���ʽ����2��ƽ�ƺ��ͼ���Ӧ�Ľ���ʽΪy=3x+2����������������ʽ��������ý������ꣻ��3��������Ϊ��2��һ����ϵ��С�ک�1��һ�κ������ɣ�

 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�