题目内容
 如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,AB=
如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,AB= ,将△ABC绕顶点C顺时针旋转至△A′B′C′的位置,且A、C、B′三点在同一条直线上,则点A经过的路线的长度是
,将△ABC绕顶点C顺时针旋转至△A′B′C′的位置,且A、C、B′三点在同一条直线上,则点A经过的路线的长度是
- A.4
- B.

- C.
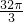
- D.
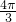
D
分析:点A经过的路线即以C为圆心,以AC的长为半径的弧.利用解直角三角形的知识求得AC的长和∠ACB的度数,从而求得∠ACA′的度数,再根据弧长公式进行计算.
解答: 解:∵将△ABC绕顶点C顺时针旋转至△A′B′C′的位置,
解:∵将△ABC绕顶点C顺时针旋转至△A′B′C′的位置,
∴∠ACB=∠A′CB′;又∵∠ABC=90°,∠BAC=30°,
∴∠ACB=∠A′CB′=60°;
∵A、C、B'三点在同一条直线上,
∴∠ACA′=120°.
又∵∠BAC=30°,AB= ,
,
∴AC=2,
∴点A经过的路线的长度= =
=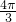 .
.
故选D.
点评:本题考查了弧长的计算、旋转的性质.搞清楚点A的运动轨迹是关键.难度中等.
分析:点A经过的路线即以C为圆心,以AC的长为半径的弧.利用解直角三角形的知识求得AC的长和∠ACB的度数,从而求得∠ACA′的度数,再根据弧长公式进行计算.
解答:
 解:∵将△ABC绕顶点C顺时针旋转至△A′B′C′的位置,
解:∵将△ABC绕顶点C顺时针旋转至△A′B′C′的位置,∴∠ACB=∠A′CB′;又∵∠ABC=90°,∠BAC=30°,
∴∠ACB=∠A′CB′=60°;
∵A、C、B'三点在同一条直线上,
∴∠ACA′=120°.
又∵∠BAC=30°,AB=
 ,
,∴AC=2,
∴点A经过的路线的长度=
 =
=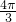 .
.故选D.
点评:本题考查了弧长的计算、旋转的性质.搞清楚点A的运动轨迹是关键.难度中等.

练习册系列答案
相关题目
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.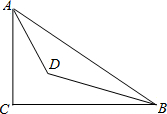 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.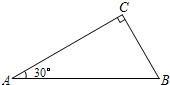 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.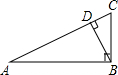 如图,在Rt△ABC中,BD⊥AC,sinA=
如图,在Rt△ABC中,BD⊥AC,sinA=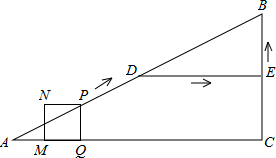 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).