题目内容
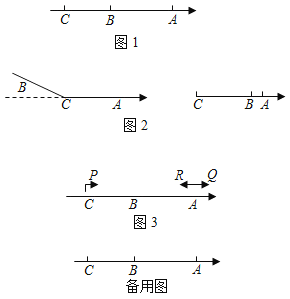
【题目】已知:OB、OC、OM、ON是∠AOD内的射线.
(1)如图1,若∠AOD=156°,OM平分∠AOB,ON平分∠BOD,∠BOD=96°,则∠MON的度数为 .
(2)如图2,若∠AOD=m°,∠NOC=23°,OM平分∠AOB,ON平分∠BOD,求∠COM的度数(用m的式子表示);
(3)如图3,若∠AOD=156°,∠BOC=22°,∠AOB=30°,OM平分∠AOC,ON平分∠BOD,当∠BOC在∠AOD内绕着点O以2°/秒的速度逆时针旋转t秒时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,求t的值.

【答案】(1)78°;(2)![]() ;(3) 当
;(3) 当![]() 或
或![]() 时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍
时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍
【解析】
(1)由OM平分∠AOB,ON平分∠BOD,得∠BOM=30°,∠BON=48°,进而即可求解;
(2)由角平分线的定义得∠BOM=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD,进而得∠MON=
∠BOD,进而得∠MON=![]() ,即可求解;
,即可求解;
(3)由题意得:∠AOM═(26+t) °,∠DON=(63﹣t) °,根据∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,列出关于t的方程,即可求解.
(1)∵∠AOD=156°,∠BOD=96°,
∴∠AOB=156°﹣96°=60°,
∵OM平分∠AOB,ON平分∠BOD,
∴∠BOM=30°,∠BON=48°,
∴∠MON=∠BOM+∠BON=78°;
(2)∵OM平分∠AOB,ON平分∠BOD,
∴∠BOM=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD,
∠BOD,
∵∠MON=∠BOM+∠BON=![]() (∠AOB+∠BOD)=
(∠AOB+∠BOD)= ![]() ∠AOD=
∠AOD=![]() ,
,
∴![]() ;
;
(3)∵∠BOC在∠AOD内绕点O以2°/秒的速度逆时针旋转t秒,
∴∠AOC=(52+2t) °,∠BOD=(126﹣2t) °,
∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM═(26+t) °,∠DON=(63﹣t) °,
当∠AOM=2∠DON时,26+t=2(63﹣t),则![]() ;
;
当∠DON=2∠AOM时,63﹣t=2(26+t),则t=![]() .
.
故当![]() 或
或![]() 时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,
时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,

 名校课堂系列答案
名校课堂系列答案