��Ŀ����
����Ŀ��������һ�����⣺̽������y��![]() ��ͼ�������ʣ�
��ͼ�������ʣ�
С�����ѧϰ�����ľ��飬�Ժ���y��![]() ��ͼ�������ʽ�����̽����
��ͼ�������ʽ�����̽����
������С���̽�����̣��벹��������
��1������y��![]() ���Ա���x��ȡֵ��Χ���� ����
���Ա���x��ȡֵ��Χ���� ����
��2���±���y��x�ļ����Ӧֵ
��x | �� | ��3 | ��2 | ��1 | �� | �� |
|
| ��1 | ��2 | ��3 | �� |
��y | �� | �� | �� | 0 | m |
| �� | �� | 0 |
| ��n | �� |
��m��n��ֵ��
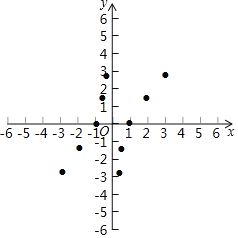
��3����ͼ����ƽ��ֱ������ϵxOy�У���������ϱ��и���ӦֵΪ����ĵ㣬��������ĵ㣬�����ú�����ͼ��
��4����Ϻ�����ͼ��д���ú��������ʣ��������ɣ���
����
���� ����
���𰸡���1��x��0����2��m=![]() ��n=
��n=![]() ����3�������������4���١�x��0ʱ������y��x����������ں���ͼ�����ԭ��Գƣ�
����3�������������4���١�x��0ʱ������y��x����������ں���ͼ�����ԭ��Գƣ�
��������
��1�����ݷ�ĸ����Ϊ0����д���Ա�����ȡֵ��Χ��
��2���ֱ����x����![]() ��3ʱ�ĺ���ֵ���ɣ�
��3ʱ�ĺ���ֵ���ɣ�
��3����������ĵ㼴�ɻ���ͼ��
��4������ͼ��д�������ʼ��ɣ�
��1������y��![]() ���Ա���x��ȡֵ��Χx��0��
���Ա���x��ȡֵ��Χx��0��
�ʴ�Ϊx��0��
��2����x����![]() ʱ��m��
ʱ��m��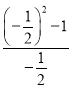 ��
��![]() ��
��
��x��3ʱ��n��![]() ��
��![]() ��
��
��3������ͼ����ͼ��ʾ��
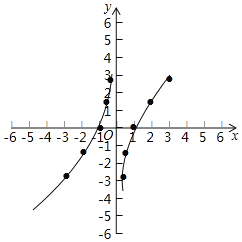
��4�����ʢ�x��0ʱ������y��x�����������
�ں���ͼ�����ԭ��Գƣ�

 ��У����ϵ�д�
��У����ϵ�д�