题目内容
 (2005•遵义)如图,在直角坐标系中,经过点A(0,2),B(2,0)和原点O(0,0)三点作⊙C,点P为⊙C上任一点(点P与点O、B不重合),则∠OPB的度数为( )
(2005•遵义)如图,在直角坐标系中,经过点A(0,2),B(2,0)和原点O(0,0)三点作⊙C,点P为⊙C上任一点(点P与点O、B不重合),则∠OPB的度数为( )分析:连接AB,OC,由90度的圆周角所对的弦为直径,得到AB为直径,即AB过点C,由OA=OB,得到三角形AOB为等腰直角三角形,得到∠OCB的度数,利用同号所对的圆周角等于所对圆心角的一半即可求出∠OPB的度数.
解答: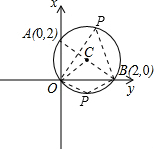 解:连接AB,由∠AOB=90°,得到AB为圆C的直径,
解:连接AB,由∠AOB=90°,得到AB为圆C的直径,
∴AB过点C,连接OC,由OA=OB,得到△AOB为等腰直角三角形,
∵C为AB的中点,
∴∠OCB=90°,
分两种情况考虑:当P在
上时,∠OPB=
∠OCB=45°;
当P在
上时,∠OPB=180°-45°=135°,
综上,∠OPB=45°或135°.
故选C.
 解:连接AB,由∠AOB=90°,得到AB为圆C的直径,
解:连接AB,由∠AOB=90°,得到AB为圆C的直径,∴AB过点C,连接OC,由OA=OB,得到△AOB为等腰直角三角形,
∵C为AB的中点,
∴∠OCB=90°,
分两种情况考虑:当P在
 |
| OPB |
| 1 |
| 2 |
当P在
 |
| OB |
综上,∠OPB=45°或135°.
故选C.
点评:此题考查了圆周角定理,等腰直角三角形的性质,熟练掌握圆周角定理是解本题的关键.

练习册系列答案
相关题目
 (2005•遵义)如图,把一个边长为6cm的正三角形剪成一个最大的正六边形,则这个正六边形的周长为
(2005•遵义)如图,把一个边长为6cm的正三角形剪成一个最大的正六边形,则这个正六边形的周长为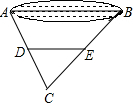 (2005•遵义)如图,A、B两点表示位于一池塘两端的两棵树,为了测量A、B两点间的距离,某同学先在地面上取一个可以直接到达A、B点C,确定AC、BC的中点D、E,并测得DE的长是15米,则A、B的距离为( )
(2005•遵义)如图,A、B两点表示位于一池塘两端的两棵树,为了测量A、B两点间的距离,某同学先在地面上取一个可以直接到达A、B点C,确定AC、BC的中点D、E,并测得DE的长是15米,则A、B的距离为( )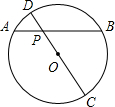 (2005•遵义)如图,⊙O中,弦AB与直径CD相交于点P,且PA=4,PB=6,PD=2,则⊙O的半径为( )
(2005•遵义)如图,⊙O中,弦AB与直径CD相交于点P,且PA=4,PB=6,PD=2,则⊙O的半径为( )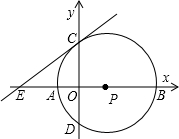 (2005•遵义)如图,点P在x正半轴上,以P为圆心的⊙P与x轴交于A、B两点,与y轴交于C、D两点,⊙P的半径是4,CD=
(2005•遵义)如图,点P在x正半轴上,以P为圆心的⊙P与x轴交于A、B两点,与y轴交于C、D两点,⊙P的半径是4,CD=