题目内容
 (2012•历下区一模)如图,△ABC是等边三角形,△DEF是边长为7的等边三角形,点B与点E重合,点A、B、(E)、F在同一条直线上,将△ABC沿E→F方向平移至点A与点F重合时停止,设点B、E之间的距离为x,△ABC与△DEF重叠部分的面积为y,则能大致反映y与x之间函数关系的图象是( )
(2012•历下区一模)如图,△ABC是等边三角形,△DEF是边长为7的等边三角形,点B与点E重合,点A、B、(E)、F在同一条直线上,将△ABC沿E→F方向平移至点A与点F重合时停止,设点B、E之间的距离为x,△ABC与△DEF重叠部分的面积为y,则能大致反映y与x之间函数关系的图象是( )分析:要找出准确反映y与x之间对应关系的图象,需分析在不同阶段中y随x变化的情况,由题意知,在△ABC移动的过程中,阴影部分总为等边三角形;据此根据重合部分的边长的不同分情况讨论求解.
解答:解:由题意知:在△ABC移动的过程中,阴影部分总为等边三角形.
当0<x≤AB时,此时重合部分为等边三角形,边长为x,则y=x×
x×
=
x2,
当AB<x≤7时,此时重合部分为等边三角形,边长为AB,则y=AB×
AB×
=
AB2,
当7<x≤7+AB时,此时重合部分重合部分为等边三角形,边长为AB+7-x,则y=(AB+7-x)×
(AB+7-x)×
;
由以上分析可知,这个分段函数的图象左边为抛物线的一部分,中间为直线的一部分,右边为抛物线的一部分.
故选B.
当0<x≤AB时,此时重合部分为等边三角形,边长为x,则y=x×
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
当AB<x≤7时,此时重合部分为等边三角形,边长为AB,则y=AB×
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
当7<x≤7+AB时,此时重合部分重合部分为等边三角形,边长为AB+7-x,则y=(AB+7-x)×
| ||
| 2 |
| 1 |
| 2 |
由以上分析可知,这个分段函数的图象左边为抛物线的一部分,中间为直线的一部分,右边为抛物线的一部分.
故选B.
点评:此题主要考查了动点问题的函数图象,主要运用分类讨论的思想,函数的知识和等边三角形的知识,具有很强的综合性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
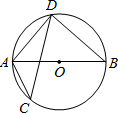 (2012•历下区一模)如图,⊙O的弦CD与直径AB相交,若∠BAD=50°,则∠ACD的度数是( )
(2012•历下区一模)如图,⊙O的弦CD与直径AB相交,若∠BAD=50°,则∠ACD的度数是( ) (2012•历下区一模)如图,将矩形纸片ABCD折叠,使点A与C重合,若∠CEB=45°,则∠CFE=
(2012•历下区一模)如图,将矩形纸片ABCD折叠,使点A与C重合,若∠CEB=45°,则∠CFE= (2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是