题目内容
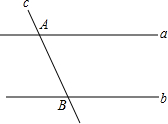 如图,a、b、c是三条公路,且a∥b,加油站M到三条公路的距离相等.
如图,a、b、c是三条公路,且a∥b,加油站M到三条公路的距离相等.(1)确定加油站M的位置.(保留作图痕迹,不写作法)
(2)一辆汽车沿公路c由A驶向B,行使到AB中点时,司机发现油料不足,仅剩15升汽油,需要到加油站加油,已知从AB中点有路可直通加油站,若AB相距200千米,汽车每行使100千米耗油12升,请判断这辆汽车能否顺利到达加油站?为什么?
分析:(1)到两条相交公路距离相等的点在这两条公路所在的直线的夹角的平分线上,那么点M是三条直线所夹角的角平分线的交点,位于AB的右侧;
(2)由角平分线易得∠AMB是直角三角形,那么斜边中点到加油站的距离等于斜边的一半,求得到加油站的距离,得到的相应的耗油量,和100千米的耗油量比较即可.
(2)由角平分线易得∠AMB是直角三角形,那么斜边中点到加油站的距离等于斜边的一半,求得到加油站的距离,得到的相应的耗油量,和100千米的耗油量比较即可.
解答: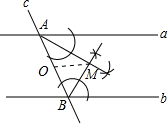 解:(1)如图所示,即点M为所求;
解:(1)如图所示,即点M为所求;
(2)能.由作图可知AM、BM分别是角平分线,又a∥b
∴△ABM是直角三角形,O是中点.
∴OM=
AB
又AB=200千米,
∴OM=100千米
汽车每行驶100千米耗油12升,12<15,
∴这辆汽车能顺利到达加油站.
 解:(1)如图所示,即点M为所求;
解:(1)如图所示,即点M为所求;(2)能.由作图可知AM、BM分别是角平分线,又a∥b
∴△ABM是直角三角形,O是中点.
∴OM=
| 1 |
| 2 |
又AB=200千米,
∴OM=100千米
汽车每行驶100千米耗油12升,12<15,
∴这辆汽车能顺利到达加油站.
点评:本题用到的知识点为:到两条相交直线距离相等的点,在这两条相交直线夹角的平分线上;直角三角形斜边上的中线,等于斜边的一半.

练习册系列答案
相关题目
 19、如图,△ABC,△ACD,△ADE是三个全等的正三角形,那么△ABC绕着顶点A沿逆时针方向至少旋转
19、如图,△ABC,△ACD,△ADE是三个全等的正三角形,那么△ABC绕着顶点A沿逆时针方向至少旋转 19、如图,l1、l2、l3是三条两两相交的公路,现需建一个仓库,要求仓库到三条公路距离相等,则仓库的可能地址有( )处.
19、如图,l1、l2、l3是三条两两相交的公路,现需建一个仓库,要求仓库到三条公路距离相等,则仓库的可能地址有( )处.
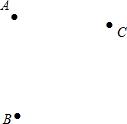 如图,A、B、C是三个城市,现要建一条环城高速公路,要求公路要经过每一个城市,且是圆形,请画出公路的路线图.(要求用直尺和圆规作图,不写出作法,保留作图痕迹并说明)
如图,A、B、C是三个城市,现要建一条环城高速公路,要求公路要经过每一个城市,且是圆形,请画出公路的路线图.(要求用直尺和圆规作图,不写出作法,保留作图痕迹并说明) 如图,OA、OB、MN是三条公路,现要在公路MN上建一个加油站H,使加油站H到公路OA,OB的距离相等.请作图表示出来.
如图,OA、OB、MN是三条公路,现要在公路MN上建一个加油站H,使加油站H到公路OA,OB的距离相等.请作图表示出来.