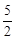题目内容
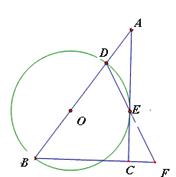
如下图,在Rt△ABC中,∠C=90°,BC=acm,AC=bcm,a>b,且a,b是方程x2-(m-1)x+(m+4)=0的两根,当AB=5cm时,(1)求a,b;
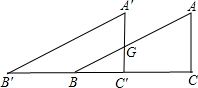
(2)若△A′B′C′与△ABC完全重合,令△ABC固定不动,将△A′B′C′沿BC所在的直线向左以每秒1cm的速度移动,几秒后两个三角形重叠部分的面积等于
| 3 | 8 |
分析:(1)可根据一元二次方程根与系数的特点,先用m表示出AB,然后再求出m,再求a,b的值;
(2)要根据相似三角形的特点来列方程求解.
(2)要根据相似三角形的特点来列方程求解.
解答:解:(1)由题意,根据一元二次方程根与系数的特点得
a+b=m-1,ab=m+4,那么a2+b2=(a+b)2-2ab=m2-4m-7=25,
∴m=8.
那么a+b=7,ab=12,根据a>b,
∴a=4,b=3.
(2)设x秒后两个三角形重叠部分的面积等于
cm2,那么BC′=4-x,C′G=
,
由题意得(4-x)×
×
=
,
解得x1=3,x2=5(不合题意,舍去),
那么3秒后两个三角形重叠部分的面积等于
cm2.
a+b=m-1,ab=m+4,那么a2+b2=(a+b)2-2ab=m2-4m-7=25,
∴m=8.
那么a+b=7,ab=12,根据a>b,
∴a=4,b=3.
(2)设x秒后两个三角形重叠部分的面积等于
| 3 |
| 8 |
| 3(4-x) |
| 4 |
由题意得(4-x)×
| 3(4-x) |
| 4 |
| 1 |
| 2 |
| 3 |
| 8 |
解得x1=3,x2=5(不合题意,舍去),
那么3秒后两个三角形重叠部分的面积等于
| 3 |
| 8 |
点评:可根据题意列出方程,判断所求的解是否符合题意,舍去不合题意的解.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
 18、如下图,在Rt△ABC中,∠C=90°,DE垂直平分AB,垂足为E,D在BC上,已知∠CAD=32°,则∠B=
18、如下图,在Rt△ABC中,∠C=90°,DE垂直平分AB,垂足为E,D在BC上,已知∠CAD=32°,则∠B=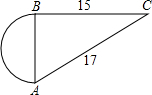 如下图,在Rt△ABC中,∠B=90°,BC=15,AC=17,以AB为直径作半圆,则此半圆的面积为
如下图,在Rt△ABC中,∠B=90°,BC=15,AC=17,以AB为直径作半圆,则此半圆的面积为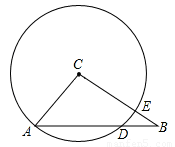
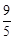 B.
B.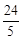 C.
C.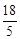 D.
D.