Question

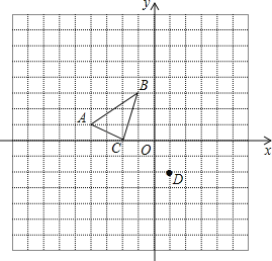
【题目】如图，三角形ABC三个顶点的坐标分别是A（-4，1），B（-1，3），C（-2，0），将三角形ABC平移得到三角形DEF，使点A与点D（1，-2）是对应点．

（1）在图中画出三角形DEF，并写出点B、C的对应点E、F的坐标；

（2）若点P在x轴上，且知三角形PCD的面积等于三角形ABC面积的，请写出满足条件的点P的坐标．

Answer 1

【答案】（1）作图见解析，点E、F的坐标分别为（4，0），（3，3）；（2）P点坐标为（1，0），（-5，0）．

【解析】

（1）利用点A和点D的坐标特征确定平移的方向和距离，利用此平移规律写出E、F点的坐标，然后描点即可；
（2）设P（m，0），先利用面积的和差求出S△ABC=，则可得到S△PCD=3，利用三角形面积公式得到×2×|m+2|=3，然后求出m即可得到P点坐标．

解：（1）如图，△DEF为所作，由图可得点E、F的坐标分别为（4，0），（3，3）；

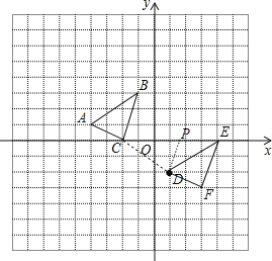
（2）设P（m，0），

S△ABC=3×3-×2×1-×3×1-×3×2=，

∵三角形PCD的面积等于三角形ABC面积的，

∴S△PCD=×=3，

∴×2×|m+2|=3，解得m=1或m=-5，

∴P点坐标为（1，0），（-5，0）．