题目内容
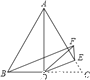
【题目】如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,∠CDE=25°,现将△CDE沿直线DE翻折得到△FDE,连接BF,则∠BFE的度数是_____.
【答案】85°
【解析】
根据等边三角形的性质可得∠C=60°,根据等腰三角形三线合一的性质可得BD=CD,根据翻折变换的性质可得CD=DF,∠DFE=∠C,∠CDE=∠FDE,从而得到BD=DF,根据等边对等角可得∠DBF=∠DFB,然后根据三角形的一个外角等于与它不相邻的两个内角的和可得∠CDF=∠DBF+∠DFB,从而求出∠DFB,再根据∠BFE=∠DFB+∠DFE计算即可得解.
解:∵△ABC是等边三角形,
∴∠C=60°,
∵AD是BC边上的中线,
∴BD=CD,
∵△CDE沿直线DE翻折得到△FDE,
∴CD=DF,∠DFE=∠C=60°,∠CDE=∠FDE=25°,
∴BD=DF,
∴∠DBF=∠DFB,
由三角形的外角性质得,∠CDF=∠DBF+∠DFB=2∠DFB,
∴∠DFB=![]() ∠CDF=∠CDE=25°,
∠CDF=∠CDE=25°,
∴∠BFE=∠DFB+∠DFE=25°+60°=85°.

练习册系列答案
相关题目