题目内容
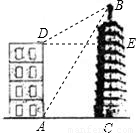
如图,大楼高30m,附近有一座塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶的仰角为30°,求塔高BC及大楼与塔之间的距离AC(结果精确到0.01m,参考数据: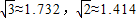 )
)
【答案】分析:设塔高BC为xm,由在Rt△ABC中,tan∠BAC=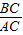 与在Rt△BDE中,tan∠BDE=
与在Rt△BDE中,tan∠BDE=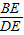 ,AC=DE,列方程即可求得x的值,继而求得塔高BC及大楼与塔之间的距离AC.
,AC=DE,列方程即可求得x的值,继而求得塔高BC及大楼与塔之间的距离AC.
解答:解:设塔高BC为xm.
在Rt△ABC中,tan∠BAC=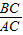 ,
,
∴AC=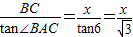 ,(2分)
,(2分)
在Rt△BDE中,tan∠BDE=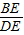 ,
,
∴DE=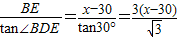 ,(4分)
,(4分)
∵AC=DE,
∴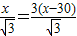 ,(6分)
,(6分)
解,得x=45(m),(8分)
这时AC=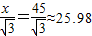 (m),(10分)
(m),(10分)
答:塔高BC为45米,大楼与塔之间的距离AC约是25.98米.(11分)
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.解此题的关键是掌握数形结合思想与方程思想的应用.
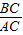 与在Rt△BDE中,tan∠BDE=
与在Rt△BDE中,tan∠BDE=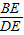 ,AC=DE,列方程即可求得x的值,继而求得塔高BC及大楼与塔之间的距离AC.
,AC=DE,列方程即可求得x的值,继而求得塔高BC及大楼与塔之间的距离AC.解答:解:设塔高BC为xm.
在Rt△ABC中,tan∠BAC=
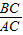 ,
,∴AC=
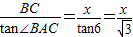 ,(2分)
,(2分)在Rt△BDE中,tan∠BDE=
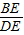 ,
,∴DE=
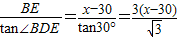 ,(4分)
,(4分)∵AC=DE,
∴
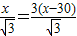 ,(6分)
,(6分)解,得x=45(m),(8分)
这时AC=
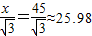 (m),(10分)
(m),(10分)答:塔高BC为45米,大楼与塔之间的距离AC约是25.98米.(11分)
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.解此题的关键是掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
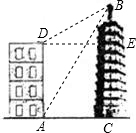 如图,大楼高30m,附近有一座塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶的仰角为30°,求塔高BC及大楼与塔之间的距离AC(结果精确到0.01m,参考数据:
如图,大楼高30m,附近有一座塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶的仰角为30°,求塔高BC及大楼与塔之间的距离AC(结果精确到0.01m,参考数据: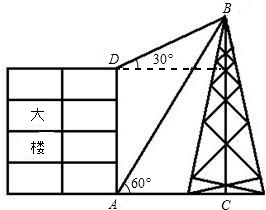
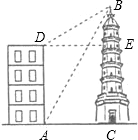 如图,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D测得塔顶的仰角为30°.则塔高BC为
如图,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D测得塔顶的仰角为30°.则塔高BC为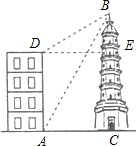 如图,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D测得塔顶的仰角为30°.求:
如图,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D测得塔顶的仰角为30°.求: