题目内容
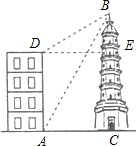 如图,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D测得塔顶的仰角为30°.求:
如图,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D测得塔顶的仰角为30°.求:(1)∠DBA的度数;
(2)塔高BC.
分析:(1)根据题意得:AD∥BC,∠BDE=30°,∠BAC=60°,∠BCA=90°,即可求得∠DBA的度数;
(2)在Rt△BDE中与Rt△ABC中,利用三角函数的正切即可得BE=DE•tan∠BDE=DE•tan30°=
DE,BC=AC•tan∠BAC=AC•tan60°=
AC,然后设BC=xm,即可求得BC的长.
(2)在Rt△BDE中与Rt△ABC中,利用三角函数的正切即可得BE=DE•tan∠BDE=DE•tan30°=
| ||
| 3 |
| 3 |
解答:解:(1)根据题意得:AD∥BC,∠BDE=30°,∠BAC=60°,∠BCA=90°,
∴∠ABC=90°-∠BAC=30°,
∴∠DBA=∠ABC=30°;
(2)在Rt△BDE中,BE=DE•tan∠BDE=DE•tan30°=
DE,
在Rt△ABC中,BC=AC•tan∠BAC=AC•tan60°=
AC,
∵AC=DE,
∴
BE=
BC,
设BC=xm,
∴
(x-30)=
x,
解得:x=45,
∴塔高BC的高为45m.
∴∠ABC=90°-∠BAC=30°,
∴∠DBA=∠ABC=30°;
(2)在Rt△BDE中,BE=DE•tan∠BDE=DE•tan30°=
| ||
| 3 |
在Rt△ABC中,BC=AC•tan∠BAC=AC•tan60°=
| 3 |
∵AC=DE,
∴
| 3 |
| ||
| 3 |
设BC=xm,
∴
| 3 |
| ||
| 3 |
解得:x=45,
∴塔高BC的高为45m.
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.解此题的关键是掌握数形结合思想与方程思想的应用.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
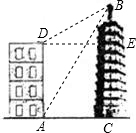 如图,大楼高30m,附近有一座塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶的仰角为30°,求塔高BC及大楼与塔之间的距离AC(结果精确到0.01m,参考数据:
如图,大楼高30m,附近有一座塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶的仰角为30°,求塔高BC及大楼与塔之间的距离AC(结果精确到0.01m,参考数据: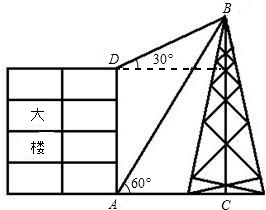
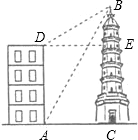 如图,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D测得塔顶的仰角为30°.则塔高BC为
如图,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D测得塔顶的仰角为30°.则塔高BC为