题目内容
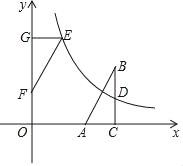
【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数y=![]() (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.求OF的长.
【答案】(1)y=![]() (2)1
(2)1
【解析】分析:(1)把点D坐标代入反比例解析式求出k的值,即可确定出表达式;
(2)由点D为BC的中点,根据点D坐标确定出BC的长,再由△ABC与△EFG成中心对称,求出DF与GE的长,由OG-GF求出OF的长即可.
详解:(1)把(3,1)代入y=![]() 中,得k=3,
中,得k=3,
则反比例函数解析式为y=![]() ;
;
(2)∵点D为BC的中点,
∴BC=2CD=2,
∵△ABC与△EFG成中心对称,
∴DF=BC=2,GE=AC=1,
在y=![]() 中,当x=1时,y=3,
中,当x=1时,y=3,
则OF=OG-GF=3-2=1.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目