��Ŀ����
����Ŀ����ͼ��AD����O��ֱ����
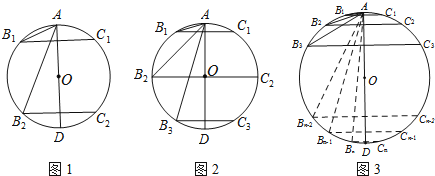
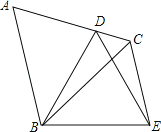
��1����ͼ1����ֱ��AD��������B1C1��B2C2��Բ��4�ȷ֣�����B1�Ķ����� ����B2�Ķ����� ��
��2����ͼ2����ֱ��AD��������B1C1��B2C2��B3C3��Բ��6�ȷ֣�����B3�Ķ����� ��
��3����ͼ3����ֱ��AD��n����B1C1��B2C2��B3 C3������BnCn��Բ��2n�ȷ֣�����Bn�Ķ����� ���ú�n�Ĵ���ʽ��ʾ��Bn�Ķ�������
���𰸡���1��22.5�㣬67.5�㣻��2��75�㣻��3��90�㩁![]() ��
��
��������
�����������1�����ÿ�����Ķ�������������Բ�ܽ����ԵĻ��Ķ�����������Բ�ܽǶ�����Բ�ܽǵĶ������������ԵĻ��Ķ�����һ�룩�ó����ɣ�
��2�����ÿ�����Ķ�������������Բ�ܽ����ԵĻ��Ķ�����������Բ�ܽǶ�����Բ�ܽǵĶ������������ԵĻ��Ķ�����һ�룩�ó����ɣ�
��3�����ÿ�����Ķ�������������Բ�ܽ����ԵĻ��Ķ�����������Բ�ܽǶ�����Բ�ܽǵĶ������������ԵĻ��Ķ�����һ�룩�ó����ɣ�
�⣺��1������ֱ��AD��������B1C1��B2C2��Բ��4�ȷ֣�
����B1C1����C1C2����B2C2����B1B2�Ķ�������90�㣬��AB1=��AC1��
����AC1�Ķ�����45�㣬
���B1=![]() ��45��=22.5�㣬
��45��=22.5�㣬
��B2=![]() ����45��+90�㣩=67.5�㣬
����45��+90�㣩=67.5�㣬
�ʴ�Ϊ��22.5�㣬67.5�㣻
��2������ֱ��AD��������B1C1��B2C2��B3C3��Բ��6�ȷ�
����B1C1����C1C2����C2C3�Ķ�������60�㣬��AB1=��AC1��
����AC1�Ķ�����30�㣬
���B3=![]() ����30��+60��+60�㣩=75�㣬
����30��+60��+60�㣩=75�㣬
�ʴ�Ϊ��75�㣻
��3������ֱ��AD��n����B1C1��B2C2��B3 C3������BnCn��Բ��2n�ȷ֣�
����B1C1����C1C2����C2C3�����Ķ������ǣ�![]() ����=��
����=��![]() ���㣬��AB1=��AC1��
���㣬��AB1=��AC1��
����AC1�Ķ����ǣ�![]() ���㣬
���㣬
���Bn=![]() ����
����![]() +
+![]() +
+![]() +��+
+��+![]() ��=
��=![]() ��[
��[![]() +
+![]() ]��=90�㩁
]��=90�㩁![]()
�ʴ�Ϊ��90�㩁![]() ��
��