题目内容
【题目】如图,△ABC是等边三角形,点D为AC边上一点,以BD为边作等边△BDE,连接CE.若CD=1,CE=3,则BC= .
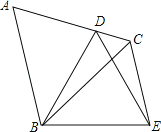
【答案】4
【解析】
试题分析:在CB上取一点G使得CG=CD,即可判定△CDG是等边三角形,可得CD=DG=CG,易证∠BDG=∠EDC,即可证明△BDG≌△EDC,可得BG=CE,即可解题.
解:在CB上取一点G使得CG=CD,

∵△ABC是等边三角形,∴∠ACB=60°,
∴△CDG是等边三角形,
∴CD=DG=CG,
∵∠BDG+∠EDG=60°,∠EDC+∠EDG=60°,
∴∠BDG=∠EDC,
在△BDG和△EDC中,
 ,
,
∴△BDG≌△EDC(SAS),
∴BG=CE,
∴BC=BG+CG=CE+CD=4,
故答案为:4.

练习册系列答案
相关题目