题目内容
【题目】如图,在直角坐标系中,点A,B分别在x,y轴上,点C是OB的中点,BE,CD都与x轴平行,BD⊥AB,∠ABO=30°.
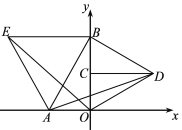
(1)判断△OBD的形状;
(2)若A(-3,0),BE=6,求证OE=AD.
【答案】(1)△OBD为等边三角形;(2)证明见详解
【解析】
(1)根据点C是OB的中点, CD与x轴平行得出![]() ,通过BD⊥AB,∠ABO=30°,求出
,通过BD⊥AB,∠ABO=30°,求出![]() 60°,即可证明△OBD为等边三角形;(2)根据BE与x轴平行得出
60°,即可证明△OBD为等边三角形;(2)根据BE与x轴平行得出![]() =90°,由∠ABO=30°,∠AOB=90°推出AB=2OA=6,则可证明
=90°,由∠ABO=30°,∠AOB=90°推出AB=2OA=6,则可证明![]()
![]() ,即可求证OE=AD.
,即可求证OE=AD.
解:(1)△OBD为等边三角形
![]() 在BOD中点C是OB的中点, CD与x轴平行
在BOD中点C是OB的中点, CD与x轴平行
∴![]()
![]()
又BD⊥AB,∠ABO=30°
∴![]() 60°
60°
∴△OBD为等边三角形
(2)![]() BE与x轴平行
BE与x轴平行
∴BE⊥BO即![]() =90°
=90°
又A(-3,0)
∴OA=3
又![]() ∠ABO=30°,∠AOB=90°
∠ABO=30°,∠AOB=90°
∴AB=2OA=6
∴AB=BE
在![]() 和
和![]() 中
中
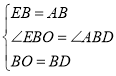
∴![]()
![]()
∴OE=AD

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目