题目内容
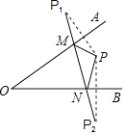
【题目】已知:如图,∠AOB内一点P,P1,P2分别P是关于OA、OB的对称点,P1P2交OA于M,交OB于N,若P1P2=6cm,则△PMN的周长是( )
A.3cmB.4cmC.5cmD.6cm
【答案】D
【解析】
由P与P1关于OA对称,得到OA为线段PP1的垂直平分线,根据线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等可得MP=MP1,同理可得NP=NP2,由P1P2=P1M+MN+NP2=6cm,等量代换可求得△PMN的周长
解:∵P与P1关于OA对称,
∴OA为线段PP1的垂直平分线,
∴MP=MP1,
同理,P与P2关于OB对称,
∴OB为线段PP2的垂直平分线,
∴NP=NP2,
∴P1P2=P1M+MN+NP2=MP+MN+NP=6cm,
∴△PMN的周长为6cm.
故选:D.

练习册系列答案
相关题目