题目内容
（2012•泸州）如图，矩形ABCD中，E是BC的中点，连接AE，过点E作EF⊥AE交DC于点F，连接AF．设| AB |
| AD |
分析：（1）由四边形ABCD是矩形，可得∠B=∠C=90°，又由EF⊥AE，利用同角的余角相等，即可求得∠BAE=∠FEC，然后利用有两角对应相等的三角形相似，证得△ABE∽△ECF；
（2）由（1），根据相似三角形的对应边成比例，可得
=
，又由E是BC的中点，即可得
=
，继而可求得tan∠BAE=tan∠EAF，即可证得AE平分∠BAF；
（3）当k=1时，可得四边形ABCD是正方形，由（1）易求得CF：CD=1：4，继而可求得AB：CD与BE：DF的值，可得△ABE与△ADF不相似．
（2）由（1），根据相似三角形的对应边成比例，可得
| EC |
| AB |
| EF |
| AE |
| BE |
| AB |
| EF |
| AE |
（3）当k=1时，可得四边形ABCD是正方形，由（1）易求得CF：CD=1：4，继而可求得AB：CD与BE：DF的值，可得△ABE与△ADF不相似．
解答：解：（1）∵四边形ABCD是矩形，
∴∠B=∠C=90°，
∴∠BAE+∠AEB=90°，
∵EF⊥AE，
∴∠AEB+∠FEC=90°，
∴∠BAE=∠FEC，
∴△ABE∽△ECF；
故（1）正确；
（2）∵△ABE∽△ECF，
∴
=
，
∵E是BC的中点，
即BE=EC，
∴
=
，
在Rt△ABE中，tan∠BAE=
，
在Rt△AEF中，tan∠EAF=
，
∴tan∠BAE=tan∠EAF，
∴∠BAE=∠EAF，
∴AE平分∠BAF；
故（2）正确；
（3）∵当k=1时，即
=1，
∴AB=AD，
∴四边形ABCD是正方形，
∴∠B=∠D=90°，AB=BC=CD=AD，
∵△ABE∽△ECF，
∴
=
=
=2，
∴CF=
CD，
∴DF=
CD，
∴AB：AD=1，BE：DF=2：3，
∴△ABE与△ADF不相似；
故（3）错误．
故选C．
∴∠B=∠C=90°，
∴∠BAE+∠AEB=90°，
∵EF⊥AE，
∴∠AEB+∠FEC=90°，
∴∠BAE=∠FEC，
∴△ABE∽△ECF；
故（1）正确；
（2）∵△ABE∽△ECF，
∴
| EC |
| AB |
| EF |
| AE |
∵E是BC的中点，
即BE=EC，
∴
| BE |
| AB |
| EF |
| AE |
在Rt△ABE中，tan∠BAE=
| BE |
| AB |
在Rt△AEF中，tan∠EAF=
| EF |
| AE |
∴tan∠BAE=tan∠EAF，
∴∠BAE=∠EAF，
∴AE平分∠BAF；
故（2）正确；
（3）∵当k=1时，即
| AB |
| AD |
∴AB=AD，
∴四边形ABCD是正方形，
∴∠B=∠D=90°，AB=BC=CD=AD，
∵△ABE∽△ECF，
∴
| AB |
| EC |
| AE |
| EF |
| BE |
| FC |
∴CF=
| 1 |
| 4 |
∴DF=
| 3 |
| 4 |
∴AB：AD=1，BE：DF=2：3，
∴△ABE与△ADF不相似；
故（3）错误．
故选C．
点评：此题考查了相似三角形的判定与性质、矩形的性质、正方形的判定与性质以及三角函数的定义．此题难度较大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
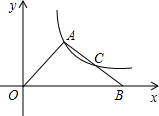（2012•泸州）如图，在△OAB中，C是AB的中点，反比例函数y=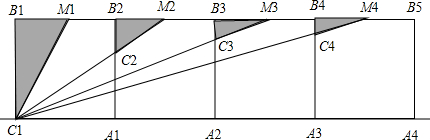
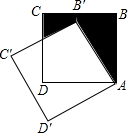（2012•泸州）如图，边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形A′B′C′D′，图中阴影部分的面积为（ ）
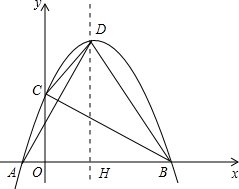侧），与y轴相交于点C，顶点D在第一象限．过点D作x轴的垂线，垂足为H．