题目内容
(2012•泸州)如图,二次函数y=-
x2+mx+m+
的图象与x轴相交于点A、B(点A在点B的左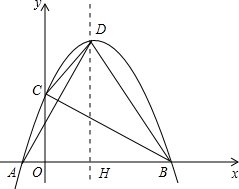 侧),与y轴相交于点C,顶点D在第一象限.过点D作x轴的垂线,垂足为H.
侧),与y轴相交于点C,顶点D在第一象限.过点D作x轴的垂线,垂足为H.
(1)当m=
时,求tan∠ADH的值;
(2)当60°≤∠ADB≤90°时,求m的变化范围;
(3)设△BCD和△ABC的面积分别为S1、S2,且满足S1=S2,求点D到直线BC的距离.
| 1 |
| 2 |
| 1 |
| 2 |
 侧),与y轴相交于点C,顶点D在第一象限.过点D作x轴的垂线,垂足为H.
侧),与y轴相交于点C,顶点D在第一象限.过点D作x轴的垂线,垂足为H.(1)当m=
| 3 |
| 2 |
(2)当60°≤∠ADB≤90°时,求m的变化范围;
(3)设△BCD和△ABC的面积分别为S1、S2,且满足S1=S2,求点D到直线BC的距离.
分析:(1)先将m=
代入y=-
x2+mx+m+
,运用配方法改写成顶点式,求出顶点D,与x轴的交点A与B的坐标,得到DH,AH的长度,再根据正切函数的定义即可求出tan∠ADH的值;
(2)先将y=-
x2+mx+m+
运用配方法改写成顶点式,求出顶点D,与x轴的交点A与B的坐标,得到DH,AH的长度,再由抛物线的对称性可知当60°≤∠ADB≤90°时,30°≤∠ADH≤45°,然后根据30°,45°角的正切函数值及锐角三角函数的增减性即可求出m的变化范围;
(3)设DH与BC交于点M,则点M的横坐标为m.先运用待定系数法求出直线BC的解析式,则可用含m的代数式表示点M的坐标,再根据S△DBC=S△ABC求出m的值,从而得出A(-1,0),B(5,0),C(0,
),S△ABC=
×6×
=
.设点D到直线BC的距离为d,根据S△DBC=
BC•d=
,即可求出d的值.
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)先将y=-
| 1 |
| 2 |
| 1 |
| 2 |
(3)设DH与BC交于点M,则点M的横坐标为m.先运用待定系数法求出直线BC的解析式,则可用含m的代数式表示点M的坐标,再根据S△DBC=S△ABC求出m的值,从而得出A(-1,0),B(5,0),C(0,
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 15 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
解答: 解:(1)∵当m=
解:(1)∵当m=
时,y=-
x2+
x+2=-
(x-
)2+
,
∴顶点D(
,
),与x轴的交点A(-1,0),B(4,0),
∴DH=
,AH=
-(-1)=
,
∴tan∠ADH=
=
=
;
(2)y=-
x2+mx+m+
=-
(x-m)2+
,
∴顶点D(m,
),
令y=-
x2+mx+m+
=0,解得:x=-1或2m+1
则与x轴的交点A(-1,0),B(2m+1,0),
∴DH=
,AH=m-(-1)=m+1,
∴tan∠ADH=
=
.
当60°≤∠ADB≤90°时,由对称性得30°≤∠ADH≤45°,
∴当∠ADH=30°时,
=
,
∴m=2
-1,
当∠ADH=45°时,
=1,
∴m=1,
∴1≤m≤2
-1;
 (3)设DH与BC交于点M,则点M的横坐标为m.
(3)设DH与BC交于点M,则点M的横坐标为m.
设过点B(2m+1,0),C(0,m+
)的直线解析式为;y=kx+b,
则
,
解得
,
即y=-
x+m+
.
当x=m时,y=-
m+m+
=
,
∴M(m,
).
∴DM=
-
=
,AB=(2m+1)-(-1)=2m+2,
又,∵S△DBC=S△ABC,
∴
•(2m+1)=(2m+2)•(m+
),
又∵抛物线的顶点D在第一象限,
∴m>0,解得m=2.
当m=2时,A(-1,0),B(5,0),C(0,
),
∴BC=
=
,
∴S△ABC=
×6×
=
.
设点D到直线BC的距离为d.
∵S△DBC=
BC•d,
∴
×
•d=
,
∴d=
.
答:点D到直线BC的距离为
.
 解:(1)∵当m=
解:(1)∵当m=| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
∴顶点D(
| 3 |
| 2 |
| 25 |
| 8 |
∴DH=
| 25 |
| 8 |
| 3 |
| 2 |
| 5 |
| 2 |
∴tan∠ADH=
| AH |
| DH |
| ||
|
| 4 |
| 5 |
(2)y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| (m+1)2 |
| 2 |
∴顶点D(m,
| (m+1)2 |
| 2 |
令y=-
| 1 |
| 2 |
| 1 |
| 2 |
则与x轴的交点A(-1,0),B(2m+1,0),
∴DH=
| (m+1)2 |
| 2 |
∴tan∠ADH=
| m+1 | ||
|
| 2 |
| m+1 |
当60°≤∠ADB≤90°时,由对称性得30°≤∠ADH≤45°,
∴当∠ADH=30°时,
| 2 |
| m+1 |
| ||
| 3 |
∴m=2
| 3 |
当∠ADH=45°时,
| 2 |
| m+1 |
∴m=1,
∴1≤m≤2
| 3 |
 (3)设DH与BC交于点M,则点M的横坐标为m.
(3)设DH与BC交于点M,则点M的横坐标为m.设过点B(2m+1,0),C(0,m+
| 1 |
| 2 |
则
|
解得
|
即y=-
| 1 |
| 2 |
| 1 |
| 2 |
当x=m时,y=-
| 1 |
| 2 |
| 1 |
| 2 |
| m+1 |
| 2 |
∴M(m,
| m+1 |
| 2 |
∴DM=
| (m+1)2 |
| 2 |
| m+1 |
| 2 |
| m(m+1) |
| 2 |
又,∵S△DBC=S△ABC,
∴
| m(m+1) |
| 2 |
| 1 |
| 2 |
又∵抛物线的顶点D在第一象限,
∴m>0,解得m=2.
当m=2时,A(-1,0),B(5,0),C(0,
| 5 |
| 2 |
∴BC=
52+(
|
5
| ||
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 5 |
| 2 |
| 15 |
| 2 |
设点D到直线BC的距离为d.
∵S△DBC=
| 1 |
| 2 |
∴
| 1 |
| 2 |
5
| ||
| 2 |
| 15 |
| 2 |
∴d=
6
| ||
| 5 |
答:点D到直线BC的距离为
6
| ||
| 5 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有运用待定系数法求函数的解析式,抛物线的顶点坐标公式,正切函数的定义,三角形的面积以及点到直线的距离的求法,综合性较强,有一定难度.其中(3)正确表示S△DBC=
DM•OB,从而根据S△DBC=S△ABC求出m的值是解题的关键.
| 1 |
| 2 |

练习册系列答案
相关题目
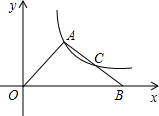 (2012•泸州)如图,在△OAB中,C是AB的中点,反比例函数y=
(2012•泸州)如图,在△OAB中,C是AB的中点,反比例函数y=
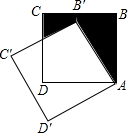 (2012•泸州)如图,边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形A′B′C′D′,图中阴影部分的面积为( )
(2012•泸州)如图,边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形A′B′C′D′,图中阴影部分的面积为( ) (2012•泸州)如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设
(2012•泸州)如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设