题目内容
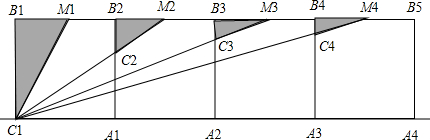
(2012•泸州)如图,n个边长为1的相邻正方形的一边均在同一直线上,点M1,M2,M3,…Mn分别为边B1B2,B2B3,B3B4,…,BnBn+1的中点,△B1C1M1的面积为S1,△B2C2M2的面积为S2,…△BnCnMn的面积为Sn,则Sn=
.(用含n的式子表示)
| 1 |
| 4(2n-1) |
| 1 |
| 4(2n-1) |

分析:由n个边长为1的相邻正方形的一边均在同一直线上,点M1,M2,M3,…Mn分别为边B1B2,B2B3,B3B4,…,BnBn+1的中点,即可求得△B1C1Mn的面积,又由BnCn∥B1C1,即可得△BnCnMn∽△B1C1Mn,然后利用相似三角形的面积比等于相似比的平方,求得答案.
解答:解:∵n个边长为1的相邻正方形的一边均在同一直线上,点M1,M2,M3,…Mn分别为边B1B2,B2B3,B3B4,…,BnBn+1的中点,
∴S1=
×B1C1×B1M1=
×1×
=
,
S△B1C1M2=
×B1C1×B1M2=
×1×
=
,
S△B1C1M3=
×B1C1×B1M3=
×1×
=
,
S△B1C1M4=
×B1C1×B1M4=
×1×
=
,
S△B1C1Mn=
×B1C1×B1Mn=
×1×
=
,
∵BnCn∥B1C1,
∴△BnCnMn∽△B1C1Mn,
∴S△BnCnMn:S△B1C1Mn=(
)2=(
)2,
即Sn:
=
,
∴Sn=
.
故答案为:
.
∴S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
S△B1C1M2=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
S△B1C1M3=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
S△B1C1M4=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 7 |
| 4 |
S△B1C1Mn=
| 1 |
| 2 |
| 1 |
| 2 |
| 2n-1 |
| 2 |
| 2n-1 |
| 4 |
∵BnCn∥B1C1,
∴△BnCnMn∽△B1C1Mn,
∴S△BnCnMn:S△B1C1Mn=(
| BnMn |
| B1Mn |
| ||
|
即Sn:
| 2n-1 |
| 4 |
| 1 |
| (2n-1)2 |
∴Sn=
| 1 |
| 4(2n-1) |
故答案为:
| 1 |
| 4(2n-1) |
点评:此题考查了相似三角形的判定与性质、正方形的性质以及直角三角形面积的公式.此题难度较大,注意掌握相似三角形面积的比等于相似比的平方定理的应用是解此题的关键.

练习册系列答案
相关题目
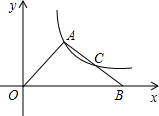 (2012•泸州)如图,在△OAB中,C是AB的中点,反比例函数y=
(2012•泸州)如图,在△OAB中,C是AB的中点,反比例函数y=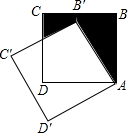 (2012•泸州)如图,边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形A′B′C′D′,图中阴影部分的面积为( )
(2012•泸州)如图,边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形A′B′C′D′,图中阴影部分的面积为( ) (2012•泸州)如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设
(2012•泸州)如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设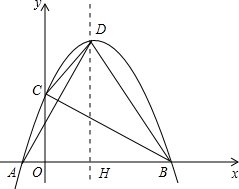 侧),与y轴相交于点C,顶点D在第一象限.过点D作x轴的垂线,垂足为H.
侧),与y轴相交于点C,顶点D在第一象限.过点D作x轴的垂线,垂足为H.