题目内容
【题目】如图，在Rt△ACB中，∠ACB=90°，BC=3，AC=4，在直线BC上找一点P，使得△ABP为以AB为腰的等腰三角形，则PC的长度为 ．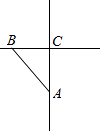 
【答案】3或7或1
【解析】解：如图： ∵在Rt△ABC中，∠C=90°，AC=4，BC=3，
∴AB= 
=5，①当AB=AP=5时，PC=BC=3；②当AB=PB=5时，PC=BC+PC=7，或PC=PB﹣BC=1；
所以答案是：3或7或1．
【考点精析】解答此题的关键在于理解等腰三角形的判定的相关知识，掌握如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等，以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
练习册系列答案
相关题目
