题目内容
【题目】如图,O是直线AB上一点,OC为任一条射线,OM平分∠AOC,ON平分∠BOC.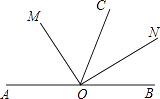
(1)图中与∠AON互补的角有;
(2)猜想∠MON的度数为 , 试说明理由.
【答案】
(1)∠CON、∠BON
(2)解:∠MON=90°,∵ON平分∠BOC,OM平分∠AOC,∴∠CON= ![]() ∠BOC,∠COM=
∠BOC,∠COM= ![]() ∠COA,∴∠MON=
∠COA,∴∠MON= ![]() ∠BOC+
∠BOC+ ![]() ∠COA=90°
∠COA=90°
【解析】解:(1)∵ON平分∠BOC,
∴∠CON=∠BON,
∵∠BON+∠AON=180°,
∴∠CON+∠AON=180°,
∴与∠AON互补的角有∠CON、∠BON,
故答案为:∠CON、∠BON;
(1)当两角之和为180°,则这两个角互补。根据图形可知∠BON和∠AON互补,根据角平分线的定义(ON平分∠BOC),得出∠CON=∠BON,即可得出与∠AON互补的角。
(2)根据角平分线的定义,分别得出∠CON与 ∠BOC,∠COM与 ∠COA的数量关系,再根据∠MON=∠CON+∠COM,即可得出结论。

练习册系列答案
相关题目