题目内容
【题目】某商店购进甲、乙两种商品,甲的进货单价比乙的进货单价高20元,已知20个甲商品的进货总价与25个乙商品的进货总价相同.
(1)求甲、乙商品的进货单价;
(2)若甲、乙两种商品共进货100件,要求两种商品的进货总价不高于9000元,同时甲商品按进价提高10%后的价格销售,乙商品按进价提高25%后的价格销售,两种商品全部售完后的销售总额不低于10480元,问有哪几种进货方案?
(3)在条件(2)下,并且不再考虑其他因素,若甲、乙两种商品全部售完,哪种方案利润最大?最大利润是多少?
【答案】(1)甲商品的进货单价是100元,乙商品的进货单价是80元;(2)有3种进货方案:①甲商品进货48件,乙商品进货52件;②甲商品进货49件,乙商品进货51件;③甲商品进货50件,乙商品进货50件(3)当甲商品进货48件,乙商品进货52件时,可获得最大利润,最大的利润是1520元.
【解析】
试题分析:(1)设甲商品的进货单价是x元,乙商品的进货单价是y元,根据“甲的进货单价比乙的进货单价高20元,已知20个甲商品的进货总价与25个乙商品的进货总价相同”列方程组,解方程组即可求解;(2)设甲商品进货x件,则乙商品进货(100﹣x)件,根据两种商品的进货总价不高于9000元,两种商品全部售完后的销售总额不低于10480元即可列不等式组求解,即可确定方案;(3)找出销售利润与x的函数关系式,利用一次函数的性质即可求解.
试题解析:(1)设甲商品的进货单价是x元,乙商品的进货单价是y元.
根据题意得:![]() ,
,
解得:x=100,y=80,
答:甲商品的进货单价是100元,乙商品的进货单价是80元;
(2)设甲商品进货x件,则乙商品进货(100﹣x)件.
根据题意得: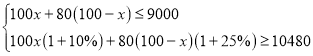 ,
,
解得:48≤x≤50.
又∵x是正整数,则x的正整数值是48或49或50,则有3种进货方案:
①商品进货48件,乙商品进货52件;
②甲商品进货49件,乙商品进货51件;
③甲商品进货50件,乙商品进货50件
(3)销售的利润w=100×10%x+80(100﹣x)×25%,即w=2000﹣10x,
则当x取得最小值48时,w取得最大值,是2000﹣10×48=1520(元).
此时,乙商品进货100﹣48=52(件).
答:当甲商品进货48件,乙商品进货52件时,可获得最大利润,最大的利润是1520元.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案