Question

【题目】如图，⊙M的半径为4，圆心M的坐标为（6，8），点P是⊙M上的任意一点，PA⊥PB，且PA、PB与x轴分别交于A、B两点，若点A、点B关于原点O对称，则AB的最小值为____．

Answer 1

【答案】12

【解析】

由Rt△APB中AB=2OP知要使AB取得最小值，则PO需取得最小值，连接OM，交⊙M于点P′，当点P位于P′位置时，OP′取得最小值，据此求解可得．

解：连接OP，
∵PA⊥PB，
∴∠APB=90°，
∵AO=BO，
∴AB=2PO，
若要使AB取得最小值，则PO需取得最小值，
连接OM，交⊙M于点P′，当点P位于P′位置时，OP′取得最小值，
过点M作MQ⊥x轴于点Q，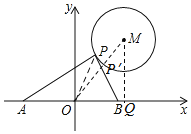

则OQ=6、MQ=8，
∴OM=10，
又∵MP′=4，
∴OP′=6，
∴AB=2OP′=12，
故答案为：12．