题目内容
 本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
甲:如图,△ABC中,AB=AC,以AB为直径作⊙O,与BC交于点D,过D作AC的垂线,垂足为E.
证明:(1)BD=DC;(2)DE是⊙O的切线.
乙:已知关于x的一元二次方程mx2-(2m-1)x+m-2=0(m>0).
(1)证明:这个方程有两个不相等的实根
(2)如果这个方程的两根分别为x1,x2,且(x1-5)(x2-5)=5m,求m的值.
解:选甲,
证明:(1)连接AD,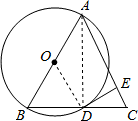
∵AB是直径,
∴AD⊥BC,
又∵AB=AC,
∴BD=CD.
(2)证明:连接OD,
∵AB=AC,BD=DC,
∴∠BAC=2∠BAD,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠BOD=∠OAD+∠ODA,
∴∠BOD=2∠BAD,
∴∠BAC=∠BOD,
∴OD∥AC,
又∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线.
分析:(1)连接AD,根据圆周角定理求出∠ADB=90°,根据等腰三角形性质推出BD=DC即可;
(2)连接OD,推出∠BAC=2∠OAD;根据OA=OD,推出∠OAD=∠ODA,根据三角形外角性质推出∠BOD=2∠BAD,得出∠BOD=∠BAC,推出OD∥AC,求出OD⊥DE即可.
点评:本题考查了等腰三角形性质,切线的判定,平行线的性质和判定,圆周角定理等知识点的运用,能综合运用定理进行推理是解此题的关键,题型比较好,具有一定的代表性.
证明:(1)连接AD,

∵AB是直径,
∴AD⊥BC,
又∵AB=AC,
∴BD=CD.
(2)证明:连接OD,
∵AB=AC,BD=DC,
∴∠BAC=2∠BAD,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠BOD=∠OAD+∠ODA,
∴∠BOD=2∠BAD,
∴∠BAC=∠BOD,
∴OD∥AC,
又∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线.
分析:(1)连接AD,根据圆周角定理求出∠ADB=90°,根据等腰三角形性质推出BD=DC即可;
(2)连接OD,推出∠BAC=2∠OAD;根据OA=OD,推出∠OAD=∠ODA,根据三角形外角性质推出∠BOD=2∠BAD,得出∠BOD=∠BAC,推出OD∥AC,求出OD⊥DE即可.
点评:本题考查了等腰三角形性质,切线的判定,平行线的性质和判定,圆周角定理等知识点的运用,能综合运用定理进行推理是解此题的关键,题型比较好,具有一定的代表性.

练习册系列答案
相关题目
选做题:本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
甲题:由山脚下的一点A测得山顶D的仰角是45°,从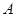 沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD. (结果保留根号)
沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD. (结果保留根号)
 |
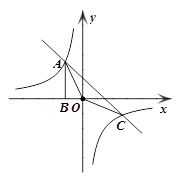
乙题:如图,Rt△ABO的顶点A是双曲线
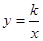 与直线
与直线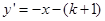 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥ 轴于B且S△ABO=
轴于B且S△ABO=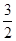 .
.
【小题1】求这两个函数的解析式
【小题2】求直线与双曲线的两个交点A、C的坐标,并写出当x在什么范围取值时,
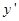 y.
y. 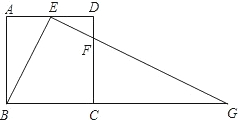
 本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分. (2012•沐川县二模)本题为选做题,从甲乙两题中选做一题即可,如果两题都做,只以甲题计分.
(2012•沐川县二模)本题为选做题,从甲乙两题中选做一题即可,如果两题都做,只以甲题计分.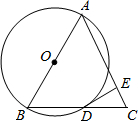 本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.