题目内容
本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.甲题:关于x的一元二次方程x2+(2k-3)x+k2=0有两个不相等的实数根α、β.
(1)求k的取值范围;
(2)若α+β+αβ=6,求(α-β)2+3αβ-5的值.
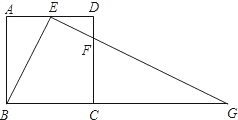
乙题:如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=
| 1 | 4 |
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
分析:甲题:(1)若方程有两个不相等的实数根,则根的判别式△=b2-4ac>0,建立关于k的不等式,即可求出k的取值范围.
(2)利用根与系数的关系,用含有k是式子表达出两根和、两根积,代入所给方程,即可确定k的值,进而求出所求代数式的值.
乙题:(1)由于ABCD为正方形,所以AD=AB=DC=BC,∠A=∠D=90°,所以AE=ED,所以
=
,又因为DF=
DC,所以
=
,所以
=
,所以△ABE∽△DEF.
(2)由于ABCD为正方形,所以ED∥BG,所以
=
,又因为DF=
DC,正方形的边长为4,所以ED=2,CG=6,所以BG=BC+CG=10.
(2)利用根与系数的关系,用含有k是式子表达出两根和、两根积,代入所给方程,即可确定k的值,进而求出所求代数式的值.
乙题:(1)由于ABCD为正方形,所以AD=AB=DC=BC,∠A=∠D=90°,所以AE=ED,所以
| AE |
| AB |
| 1 |
| 2 |
| 1 |
| 4 |
| DF |
| DE |
| 1 |
| 2 |
| AE |
| AB |
| DF |
| DE |
(2)由于ABCD为正方形,所以ED∥BG,所以
| ED |
| CG |
| DF |
| CF |
| 1 |
| 4 |
解答:甲题:
解:(1)∵方程x2+(2k-3)x+k2=0有两个不相等的实数根,
∴△>0,即(2K-3)2-4×1×K2>0,
解得:k<
;
(2)由根与系数的关系得:α+β=-(2k-3),αβ=k2,
∵α+β+αβ=6,
∴k2-2k+3-6=0,
解得k=3或k=-1,
由(1)可知:k=3不合题意,舍去.
∴k=-1,
∴α+β=5,αβ=1
故(α-β)2+3αβ-5=(α+β)2-αβ-5=19.
乙题:
(1)证明:∵ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90°,
∵AE=ED,
∴
=
,
又∵DF=
DC,
∴
=
,
∴
=
,
∴△ABE∽△DEF.
(2)解:∵ABCD为正方形,
∴ED∥BG,∴
=
,
又∵DF=
DC正方形的边长为4,
∴ED=2,CG=6,
BG=BC+CG=10.
解:(1)∵方程x2+(2k-3)x+k2=0有两个不相等的实数根,
∴△>0,即(2K-3)2-4×1×K2>0,
解得:k<
| 3 |
| 4 |
(2)由根与系数的关系得:α+β=-(2k-3),αβ=k2,
∵α+β+αβ=6,
∴k2-2k+3-6=0,
解得k=3或k=-1,
由(1)可知:k=3不合题意,舍去.
∴k=-1,
∴α+β=5,αβ=1
故(α-β)2+3αβ-5=(α+β)2-αβ-5=19.
乙题:
(1)证明:∵ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90°,
∵AE=ED,
∴
| AE |
| AB |
| 1 |
| 2 |
又∵DF=
| 1 |
| 4 |
∴
| DF |
| DE |
| 1 |
| 2 |
∴
| AE |
| AB |
| DF |
| DE |
∴△ABE∽△DEF.
(2)解:∵ABCD为正方形,
∴ED∥BG,∴
| ED |
| CG |
| DF |
| CF |
又∵DF=
| 1 |
| 4 |
∴ED=2,CG=6,
BG=BC+CG=10.
点评:甲题主要考查了一元二次方程根与系数的关系及根的判别式,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.
乙题主要考查根据相似三角形的判定定理判定三角形相似.
乙题主要考查根据相似三角形的判定定理判定三角形相似.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
选做题:本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
甲题:由山脚下的一点A测得山顶D的仰角是45°,从 沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD. (结果保留根号)
沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,求山高CD. (结果保留根号)
 |
乙题:如图,Rt△ABO的顶点A是双曲线
 与直线
与直线 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥ 轴于B且S△ABO=
轴于B且S△ABO= .
.
【小题1】求这两个函数的解析式
【小题2】求直线与双曲线的两个交点A、C的坐标,并写出当x在什么范围取值时,
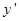 y.
y. 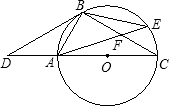 本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分. (2012•沐川县二模)本题为选做题,从甲乙两题中选做一题即可,如果两题都做,只以甲题计分.
(2012•沐川县二模)本题为选做题,从甲乙两题中选做一题即可,如果两题都做,只以甲题计分. 本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.