题目内容
你能求(x—1)(x99+x98+x97+……+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形入手。分别计算下列各式的值:
(1)(x—1)(x+1)=x2-1;
(2)(x—1)(x2+x+1)= x3-1;
(3)(x—1)(x3+x2+x+1)= x4-1;
……
由此我们可以得到:
(x—1)(x99+x98+x97+……+x+1)=____________;
请你利用上面的结论,完成下面两题的计算:
(1)299+298+297+……+2+1;
(2)(—2)50+(—2)49+(—2)48+……+(-2)+1.
遇到这样的问题,我们可以先思考一下,从简单的情形入手。分别计算下列各式的值:
(1)(x—1)(x+1)=x2-1;
(2)(x—1)(x2+x+1)= x3-1;
(3)(x—1)(x3+x2+x+1)= x4-1;
……
由此我们可以得到:
(x—1)(x99+x98+x97+……+x+1)=____________;
请你利用上面的结论,完成下面两题的计算:
(1)299+298+297+……+2+1;
(2)(—2)50+(—2)49+(—2)48+……+(-2)+1.
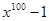 ;(1)
;(1)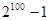 ;(2)
;(2)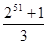
试题分析:根据平方差公式,和立方差公式可得前2个式子的结果,利用多项式乘以多项式的方法可得出第3个式子的结果;从而总结出规律是(x-1)(x99+x98+x97+…+x+1)=x100-1,根据上述结论计算下列式子即可.
由题意得(x-1)(x99+x98+x97+…+x+1)=x100-1.
(1)299+298+297+…+2+1=(2-1)(299+298+297+…+2+1)=2100-1;
(2)(-2)50+(-2)49+(-2)48+…(-2)+1
=
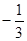 (-2-1)[(-2)50+(-2)49+(-2)48+…(-2)+1]
(-2-1)[(-2)50+(-2)49+(-2)48+…(-2)+1]=
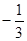 (-251-1)
(-251-1)=
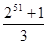 .
.点评:规律型的问题一般是从所给的数据和运算方法进行分析,从特殊值的规律上总结出一般性的规律.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目




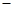 2m= .
2m= . ,
, ,求
,求 =_ _
=_ _
 .
.