题目内容
已知A、E、C三点在同一直线上,线段AC=8,线段CE=6,点B、D分别是线段AC、CE的中点,求线段BD的长度.
分析:分为两种情况,画出图形,求出BC、CD长,即可求出答案.
解答:解:分为两种情况:①如图1,E在线段AC延长线上时,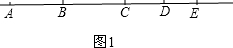
∵AC=8,CE=6,点B、D分别是线段AC、CE的中点,
∴BC=
AC=4,CD=
CE=3,
∴BD=BC+CD=4+3=7;
②如图2,E在线段AC上时,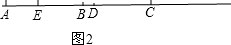
∵AC=8,CE=6,点B、D分别是线段AC、CE的中点,
∴BC=
AC=4,CD=
CE=3,
∴BD=BC-CD=4-3=1;
即线段BD的长度是7或1.

∵AC=8,CE=6,点B、D分别是线段AC、CE的中点,
∴BC=
| 1 |
| 2 |
| 1 |
| 2 |
∴BD=BC+CD=4+3=7;
②如图2,E在线段AC上时,
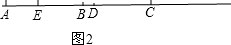
∵AC=8,CE=6,点B、D分别是线段AC、CE的中点,
∴BC=
| 1 |
| 2 |
| 1 |
| 2 |
∴BD=BC-CD=4-3=1;
即线段BD的长度是7或1.
点评:本题考查了求两点之间的距离的应用,主要考查学生的计算能力,注意:要进行分类讨论啊.

练习册系列答案
相关题目

 如图,已知A,O,B三点在同一条直线上,OD平分∠BOC,OE平分∠AOC.试判断射线OE与射线OD的位置关系,并说明理由.
如图,已知A,O,B三点在同一条直线上,OD平分∠BOC,OE平分∠AOC.试判断射线OE与射线OD的位置关系,并说明理由. 如图,已知B、C、D三点在同一条直线上,∠B=∠1,∠2=∠E,说明AC∥ED.
如图,已知B、C、D三点在同一条直线上,∠B=∠1,∠2=∠E,说明AC∥ED.