题目内容
【题目】矩形ABCD的对角线相交于点O,AC=![]() ,CD=1,
,CD=1,
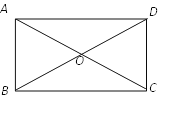
(1)尺规作图:作∠ABC的平分线交AD于点E,连结CE;
(2)判断线段BE与CE的关系,并证明你的判断.
【答案】(1)作图见解析(2) 证明见解析
【解析】试题分析:(1)根据基本作图——作角的平分线即可;
(2)先根据勾股定理求出AD的长,然后根据角平分线的性质(角平分线上的点到角的两边的距离相等)和判定(到角的两边距离相等的点在角的平分线上)证出BE=CE.
试题解析:(1)如图所示
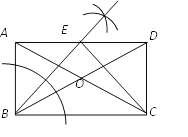
(2) BE⊥CE且BE=CE 理由如下:
∵矩形ABCD中,
∴∠BAD=∠ADC =∠ABC= 90°,AB=CD,AD∥BC.
∴在Rt△ADH中,AC=![]() ,CD=1,
,CD=1,
∴![]()
∵BE平分∠ABC
∴∠ABE=∠EBC= 45°
∵AD∥BC
∴∠AEB=∠EBC
∴∠AEB=∠ABE= 45°
∴AB=AE
∵AB=CD
∴AE=AB=1,DE=AD-AE=1
∴AE=DE
∴△DAB≌△DEB(SAS),
∴BE=CE且∠CED=∠AEB= 45°.
∴∠BED=180°-∠AEB-∠CED = 90°
∴BE⊥CE且BE=CE

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目